Методы расчета нелинейных цепей переменного тока на основе ВАХ для эквивалентных синусоид
Замена несинусоидальных функций i(t) и u(t) эквивалентными синусоидальными позволяет применить к расчету нелинейных цепей переменного тока комплексный метод со всеми вытекающими из него преимуществами.
В простейших случаях, когда схема цепи состоит только из последовательно или только из параллельно включенных элементов, решение задачи может быть выполнено графически методом сложения ВАХ. Отличительной особенностью данного метода является то обстоятельство, что отдельные ВАХ складываются не арифметически, как это имело место в цепях постоянного тока, а векторно в соответствии с уравнениями Кирхгофа в комплексной (векторной) форме.
 Пусть требуется рассчитать режим нелинейной цепи с последовательным соединением источника ЭДС Е, линейного резистора R и нелинейной катушки с ВАХ UL(I) (рис. 227а)
Пусть требуется рассчитать режим нелинейной цепи с последовательным соединением источника ЭДС Е, линейного резистора R и нелинейной катушки с ВАХ UL(I) (рис. 227а)
|
Построим в одной системе координат U-I графические диаграммы ВАХ отдельных элементов: резистора UR=IR и катушки UL(I). Векторное сложение ВАХ отдельных элементов по оси U следует выполнить в соответствии со вторым законом Кирхгофа 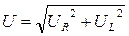 , в результате сложения получим результирующую ВАХ U(I) (рис. 227б). Положение рабочей точки n на результирующей ВАХ определяется условием U=E. Последовательность графического решения показана на рис. 227б стрелками.
, в результате сложения получим результирующую ВАХ U(I) (рис. 227б). Положение рабочей точки n на результирующей ВАХ определяется условием U=E. Последовательность графического решения показана на рис. 227б стрелками.
Та же задача может быть решена аналитически методом последовательных приближений. Так как в аналитических методах расчета используется математическая форма ВАХ, то заданную ВАХ нелинейной катушки аппроксимируем одним из уравнений, например I=aU+bU5.
Составляется схема вычислений:

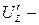 задаются в первом приближении. Далее следуют вычисления:
задаются в первом приближении. Далее следуют вычисления:
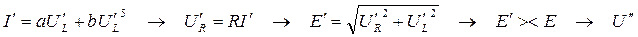 и т. д. до достижения требуемой точности, например,
и т. д. до достижения требуемой точности, например, 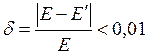 .
.
Метод последовательных приближений применим к расчету схем любой сложности. Вычисления в отдельном цикле для сложных схем выполняются в комплексной форме. В качестве примера приведем расчет схемы рис. 228. Заданы параметры линейных элементов Е, R, XC. ВАХ нелинейных элементов заданы аналитически в виде уравнений аппроксимации: 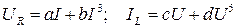 .
.

Для исследуемой схемы система комплексных уравнений Кирхгофа совместно с уравнениями аппроксимации имеет вид:

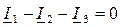 (1)
(1)
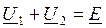 (2)
(2)
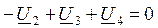 (3)
(3)
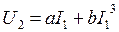 (4)
(4)
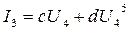 (5)
(5)
Один из вариантов решения полученной системы уравнений методом последовательных приближений представлен ниже.
1) Задаются в первом приближении комплексным напряжением на нелинейной катушке, например: 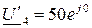 .
.
2) Определяется модуль тока 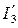 аналитически из уравнения (5) или графически по диаграмме функции IL(UL). Аргумент этого комплекса принимается равным -90о(в катушке ток отстает от напряжения на угол j=90о). В комплексной форме
аналитически из уравнения (5) или графически по диаграмме функции IL(UL). Аргумент этого комплекса принимается равным -90о(в катушке ток отстает от напряжения на угол j=90о). В комплексной форме 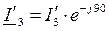 .
.
3) Определяется напряжение на линейном резисторе по закону Ома: 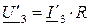 .
.
4) Из уравнения (3) находится напряжение на конденсаторе: 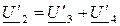 .
.
5) По закону Ома определяется ток конденсатора: 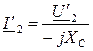 .
.
6) Из уравнения (1) находится ток источника 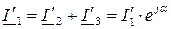 .
.
7) Определяется модуль напряжения 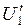 аналитически из уравнения (4) или графически по диаграмме функции UR(IR). Аргумент этого комлекса принимается равным аргументу комплекса тока
аналитически из уравнения (4) или графически по диаграмме функции UR(IR). Аргумент этого комлекса принимается равным аргументу комплекса тока 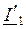 (в резисторе ток совпадает с напряжением). В комплексной форме
(в резисторе ток совпадает с напряжением). В комплексной форме 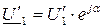 .
.
8) Из уравнения (2) находится расчетное значение ЭДС: 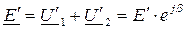 .
.
9) Сравнивают найденное в первом приближении значение модуля ЭДС 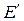 с заданным значением ЭДС Е и с учетом вида полученного неравенства
с заданным значением ЭДС Е и с учетом вида полученного неравенства 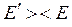 задаются новым значением напряжения
задаются новым значением напряжения 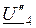 во втором приближении и повторяют расчет по тому же алгоритму. Циклы расчета (итерации) повторяют до достижения желаемой точности. В результатах последнего цикла корректируют аргументы комплексных токов и напряжений путем добавления к ним значения -b.
во втором приближении и повторяют расчет по тому же алгоритму. Циклы расчета (итерации) повторяют до достижения желаемой точности. В результатах последнего цикла корректируют аргументы комплексных токов и напряжений путем добавления к ним значения -b.
Дата добавления: 2020-07-18; просмотров: 609;











