Векторная диаграмма и схема замещения катушки с ферромагнитным сердечником
Рассмотрим процессы в катушке с замкнутым ферромагнитным сердечником, обмотка которой имеет w витков.Уравнение, описывающее процесс в катушке, имеет вид
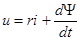 ,
,
где r — сопротивление обмотки.
Полное потокосцепление представим в виде суммы 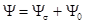 .
.
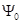 – потокосцепление, определяемое линиями магнитной индукции, замыкающимися целиком вдоль сердечника. Следовательно,
– потокосцепление, определяемое линиями магнитной индукции, замыкающимися целиком вдоль сердечника. Следовательно, 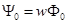 , где
, где 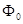 – поток сквозь сечение сердечника, определяемый этими линиями.
– поток сквозь сечение сердечника, определяемый этими линиями.
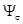 – потокосцепление, определяемое линиями магнитной индукции, замыкающимися частично или полностью в воздухе. Это потокосцепление пропорционально току:
– потокосцепление, определяемое линиями магнитной индукции, замыкающимися частично или полностью в воздухе. Это потокосцепление пропорционально току: 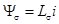 . Так как магнитное сопротивление пути, по которому замыкаютсялинии потока, практически не зависит от тока и, следовательно, индуктивность
. Так как магнитное сопротивление пути, по которому замыкаютсялинии потока, практически не зависит от тока и, следовательно, индуктивность 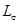 постоянна. Потокосцепление
постоянна. Потокосцепление 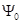 нелинейносвязано с током i, так как магнитная проницаемость и, следовательно, магнитное сопротивление сердечника зависят от напряженностимагнитного поля.
нелинейносвязано с током i, так как магнитная проницаемость и, следовательно, магнитное сопротивление сердечника зависят от напряженностимагнитного поля.
Уравнение катушки теперь можно переписать в виде:
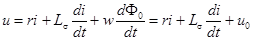 .
.
Это уравнение нелинейное. Поэтому, даже если приложенное напряжение и синусоидально, ток i будет несинусоидальным. Заменяя несинусоидальные кривые тока и потока эквивалентными синусоидами, можем записать это уравнение в комплексной форме для комплексных амплитуд:
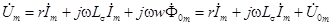 .
.
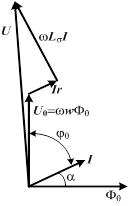
| Эквивалентная синусоида тока отстает от эквивалентной синусоиды напряжения 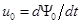 на угол на угол 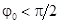 вследствие наличия потерь в сердечнике. Таким образом, эквивалентная синусоида потока вследствие наличия потерь в сердечнике. Таким образом, эквивалентная синусоида потока 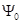 отстает от эквивалентной синусоиды тока i на угол отстает от эквивалентной синусоиды тока i на угол 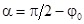 , так как эквивалентная синусоида потока , так как эквивалентная синусоида потока 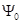 отстает от эквивалентной синусоиды напряжения отстает от эквивалентной синусоиды напряжения 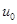 на угол на угол 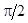 . .
| |
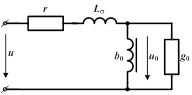
| Соответственно катушку можно представить в виде эквивалентной схемы, в которой проводимости определяют как
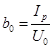 , , 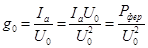 . .
| |
Процессы в такой эквивалентной цепи, распределение токов и напряжений такое же, как и в реальном устройстве.
Дата добавления: 2019-12-09; просмотров: 811;











