И методов их исследования

Нелинейные цепи переменного тока могут содержать в своей структуре нелинейные элементы любого рода: нелинейные резисторы u(i), нелинейные ка­тушки ψ(i) и нелинейные конденсаторы q(u). Физические характеристики нели­нейных элементов на переменном токе могут существенно отличаться от их аналогичных характеристик на постоянном токе.

Существуют нелинейные элементы, у которых время установления ре­жима соизме­римо с периодом переменного тока, т.е. проявляется инерцион­ность. По этому показателю все нелинейные элементы разделяют на инерцион­ные и безинерционные.

К инерционным относятся те нелинейные элементы, нелинейность харак­теристик ко­торых обусловлена температурным режимом (лампы накаливания, термисторы). Установле­ние температурного режима в таких элементах требует некоторого времени. Температура и, следовательно, сопротивление такого эле­мента определяется действующим значением тока в нем. Таким образом, для действующих значений тока и напряжения инерционный элемент является не­линейным, а для мгновенных значений в интервале периода - линейным.

Физические характеристики безинерционных нелинейных элементов ос­таются прак­тически неизменными в широком диапазоне частот. Нелинейность таких элементов проявля­ется как для действующих, так и для мгновенных зна­чений величин. Нелинейность физиче­ских характеристик приводит к искаже­нию форм кривых физических величин на зажимах таких элементов. Так, на­пример, при синусоидальном напряжении на зажимах безинерцион­ного нели­нейного резистора ток в нем будет несинусоидальным и, наоборот, при сину­сои­дальном токе напряжение на его зажимах будет несинусоидальным. К без­инерционным не­линейным элементам относят полупроводниковые приборы: диоды, туннельные диоды, транзисторы, стабилитроны, тиристоры и др.

Статическими характеристиками нелинейных элементов называются со­ответствую­щие зависимости u(i) – для резистора, ψ(і) – для катушки, q(u) - для конденсатора, получен­ные при медленном изменении переменных.

Динамическими характеристиками нелинейных элементов называются те же зависи­мости u(i) , ψ(і) , q(u) , но полученные при быстрых изменениях пере­менных.

При сравнительно невысоких частотах динамические характеристики практически совпадают со статическими. Cущественные различия этих харак­теристик начинают прояв­ляться в области высоких частот (радиочастот).

Электромагнитные процессы в нелинейной цепи переменного тока могут быть опи­саны системой нелинейных дифференциальных уравнений, составлен­ных для схемы цепи по уравнениям Кирхгофа. В математике не существует об­щих методов решения таких систем уравнений и, следовательно, не существует общих методов расчета нелинейных цепей пере­менного тока.

Все задачи по расчету нелинейных цепей переменного тока в установив­шемся режиме можно разделить на две группы.

К первой группе задач относятся такие, в которых целью расчета является определе­ние действующих значений токов и напряжений. Такие задачи встре­чаются в электроэнерге­тике, где искажение форм кривых токов и напряжений незначительны и не играют сущест­венную роль, а определяются действующие значения этих величин.

Ко второй группе задач относятся такие, в которых целью расчета явля­ется определе­ние мгновенных значений токов и напряжений, а также форм кри­вых и гармонических спек­тров функций. Такие задачи встречаются в электро­нике, где принцип действия устройств основан на преобразовании форм кри­вых переменных с помощью нелинейных характери­стик элементов.

Методы решения задач первой и второй групп могут существенно отли­чаться.

2. Замена несинусоидальных функций u(t) и i(t) эквивалентными

сину­соидаль­ными

В электрических цепях электроэнергетики, содержащих нелинейные эле­менты, иска­жение форм кривых токов и напряжений незначительны, играют второстепенную роль и ими можно пренебречь. Для исследования таких цепей можно применять так называемый метод эквивалентных синусоид. Сущность метода состоит в том, что при незначительных искаже­ниях форм кривых неси­нусоидальные функции токов и напряжений i(t) и u(t) заменяются эквивалент­ными по действующему значению синусоидальными функциями (рис. 226а, б).

При малых искажениях форм кривых высшие гармоники практически не влияют на величину действующего значения функции, поэтому действующее значение несинусоидальной функ­ции практически равно действующему значе­нию ее первой гармоники.

При переходе к эквивалентным синусоидам происходит полная потеря информации о формах кривых функций, их гармонических составах, максиму­мах и минимумах и т. д.

При расчете нелинейных цепей методом эквивалентных синусоид физи­ческие харак­теристики нелинейных элементов u(t) – для резистора, ψ(і) – для катушки и q(u) - для кон­денсатора заменяются расчетными вольтамперными характеристиками U(I) или I(U) для дей­ствующих значений эквивалентных си­нусоидальных величин. Расчетные ВАХ для конкрет­ных линейных элементов могут быть получены экспериментально путем проведения изме­рений дейст­вующих значений U и I в произвольном режиме. Если заданы физические ха­рак­теристики для мгновенных значений величин, то соответствующие ВАХ мо­гут быть полу­чены расчетным путем для синусоидального режима по напряже­нию или току. Например, пусть веберамперная характеристика нелинейной ка­тушки выражается уравнением i(ψ)=аψ + bψ⁵. При синусоидальном напряжении на зажимах катушки 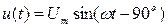ее по­токосцепление также будет из­меняться по синусоидальному закону :

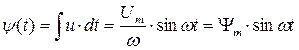, где .

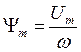Закон изменения тока в катушке получим из уравнения аппроксимации:

.

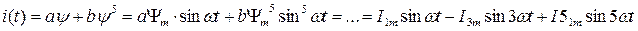Действующее значение тока будет равно: .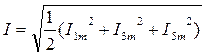

Следует иметь в виду тот факт, что ВАХ U(I) нелинейных элементов, сня­тые экспе­риментально или полученные расчетным путем, соответствуют опре­деленному режиму, при котором они были получены, например, синусоидаль­ному напряжению. В условиях конкрет­ной цепи напряжение на этих элементах могут существенно отличаться от синусоидальной формы, поэтому реальные ВАХ могут несущественно отличаться от экспериментальных или расчетных.