Расчет разветвленной магнитной цепи
Расчет разветвленных магнитных цепей может выполнятся графическим или аналитическим методами точно так же, как и нелинейных электрических цепей.
Пример 1. Заданы геометрические размеры разветвленной магнитной цепи (рис. 23а) и основная кривая намагничивания В=f(Н) для материала магнитопровода.
Графическое решение задачи выполняется в следующей последовательности.
1. Магнитная цепь разбивается на однородные участки и согласно этой разбивке составляется эквивалентная схема (рис. 220б).
2. На основе заданных геометрических размеров (l, S) и основной кривой намагничивания В=f(Н) выполняется расчет ВАХ для каждого выделенного участка цепи по форме 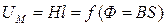 . Результаты расчета ВАХ сводятся для удобства пользования в общую таблицу.
. Результаты расчета ВАХ сводятся для удобства пользования в общую таблицу.
3.

4. В одной системе координат в выбранных масштабах для Ф и U стоятся графические диаграммы ВАХ для отдельных участков цепи (рис. 221).

5. Выполняется графическое сложение ВАХ отдельных участков в соответствии с порядком свертки эквивалентной схемы:
а). ВАХ U2(Ф2) и U0(Ф2) складываются последовательно (по оси U), в результате их сложения получается ВАХ (U2+ U0);
б). ВАХ (U2+ U0) и U3(Ф3) складываются параллельно (по оси Ф ), в результате их сложения получается ВАХ (Ф2+Ф3);
в). ВАХ U1(Ф1) и (Ф2+Ф3) складываются последовательно (по оси U ), в результате их сложения получается входная ВАХ Iw(Ф1);
5. На входной ВАХ Iw(Ф1) для заданного значения Iw определяется положение рабочей точки n, после чего проводится графическое определение остальных величин (решение показано стрелками на рис. 221).
Пример 2. Заданы геометрические размеры разветвленной магнитной цепи (рис. 222а) и основная кривая намагничивания В=f(Н) для материала магнитопровода.
Аналитическое решение задачи выполняется в следующей последовательности.
1. Магнитная цепь разбивается на однородные участки и согласно этой разбивке составляется эквивалентная схема (рис. 222б). Направления МДС на схеме определяются по правилу правоходового винта.
2. На основе заданных геометрических размеров (l, S) и основной кривой намагничивания В=f(Н) выполняется расчет ВАХ для отдельных участков цепи. Результаты расчета ВАХ сводятся для удобства пользования в общую таблицу.

3.ВАХ отдельных участков [U1(Ф1), U2(Ф2), U3(Ф3)] аппроксимируются выбранным уравнением, например, уравнением гиперболического синуса: 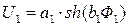 ,
, 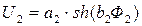 ,
, 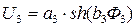 , определяются коэффициенты аппроксимации a1, b1, a2, b2, a3, b3.
, определяются коэффициенты аппроксимации a1, b1, a2, b2, a3, b3.
4.Составляется система нелинейных уравнений (по законам Кирхгофа или по методу двух узлов) для эквивалентной схемы цепи:
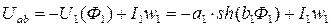 (1)
(1)
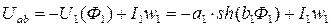 (2)
(2)
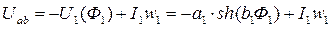 (3)
(3)
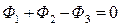 (4)
(4)
5. Система нелинейных алгебраических уравнений решается методом последовательных приближений на ЭВМ. Составляется алгоритм (блок-схема) решения, в соответствии с которым составляется программа. Один из возможных вариантов алгоритма вычислений для рассматриваемого примера приведен ниже.
1) Задаются в первом приближении магнитным напряжением между узлами схемы Uab1 (начало главного цикла).
2) Для решения нелинейного уравнения (1) создается 1-й частный цикл вычислений: задаются 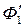 (первое приближение); из (1) Þ
(первое приближение); из (1) Þ 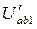 ;
; 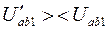 ; задаются
; задаются 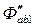 и т.д., в итоге находят Ф11.
и т.д., в итоге находят Ф11.
3) Для решения нелинейного уравнения (2) создается 2-й частный цикл вычислений: задаются 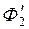 (первое приближение); из (2) Þ
(первое приближение); из (2) Þ 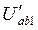 ;
; 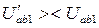 ; задаются
; задаются 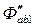 и т.д., в итоге находят Ф21.
и т.д., в итоге находят Ф21.
4) Для решения нелинейного уравнения (3) создается 3-й частный цикл вычислений: задаются 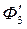 (первое приближение); из (3) Þ
(первое приближение); из (3) Þ 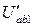 ;
; 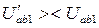 ; задаются
; задаются 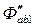 и т.д., в итоге находят Ф31.
и т.д., в итоге находят Ф31.
5) Решается уравнение (4): 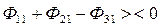 (конец главного цикла).
(конец главного цикла).
Задаются Uab2 (второе приближение) и повторяют вычисления до достижения требуемой точности.
В соответствии с алгоритмом составляется программа вычислений на любом алгоритмическом языке для ЭВМ.
Решение рассматриваемой задачи может быть выполнено графически подобно примеру 1.
Недостатками графического метода расчета являются его низкая точность и большая трудоемкость. С другой стороны, решение той же задачи на ЭВМ методом последовательных приближений требует дополнительных затрат на составление и отладку программы для ЭВМ.
Дата добавления: 2020-07-18; просмотров: 679;











