Расчет магнитной цепи с постоянным магнитом

Постоянные магниты находят применение в автоматике, измерительной технике и других отраслях для получения постоянных магнитных полей. В ос­нове их принципа дейст­вия лежит физическое явление остаточного намагничи­вания. Известно, что любой ферромаг­нитный материал, будучи намагниченным от внешнего источника, способен сохранять неко­торые остатки магнитного поля после снятия внешней намагничивающей силы. Ферромаг­нитные мате­риалы, способные длительное время сохранять остаточное поле, получили на­звание магнитотвердых. К таким материалам относятся сплавы из ферромаг­нитных металлов магнико (Ma, Ni, Co) и альнико (Al, Ni, Co). Из магнитотвер­дых материалов изготавливаются постоянные магниты различных конструктив­ных форм.

Ферромагнитные материалы, имеют широкую петлю гистерезиса (рис. 223), стенка кото­рой и является кривой размагничивания В(Н) и приводится в спра­вочной литературе.

Пусть требуется рассчитать магнитную цепь, состоящую из постоянного магнита (l₁, S₁), магнитопровода (l₂, S₂) и зазора (S₂, 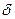) (рис. 224а). Геометриче­ские размеры, кривая раз­магничивания для постоянного магнита В₁(Н₁) и ос­новная кривая намагничивания В₂(Н₂) для магнитопровода заданы. Схема заме­щения цепи представлена на рис. 27б.

Ниже приводится графическое решение задачи.

1.На основе заданных геометрических размеров (l, s) и кривых намагни­чивания В=f(Н) производится расчет ВАХ для отдельных участков цепи: U₁(Ф), U₂(Ф) и U₀(Ф).

2.В одной системе координат в выбранных масштабах строятся графиче­ские диа­граммы ВАХ отдельных участков (рис. 225).

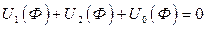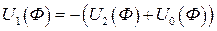3.По 2-ому закону Кирхгофа для схемы цепи: или . Согласно полученному уравнению складыва­ются последова­тельно (по оси U) ВАХ U₂(Ф) и U₀(Ф), в результате сложения получается ВАХ (U₂+U₀). По­лученная суммарная ВАХ обращается относи­тельно оси Ф (знак - ) (рис. 225). Точка пересече­ния обращенной ВАХ с ВАХ U₁(Ф) определяет положение рабочей точки n. Дальнейшее ре­шение задачи по­казана стрелками.