Графический метод расчета простых нелинейных цепей
Сущность графического метода расчета состоит в том, что решение нелинейных уравнений, составленных для схемы по законам Кирхгофа, выполняется графически путем графического сложения соответствующих ВАХ элементов.
Пусть нелинейная цепь состоит из двух нелинейных элементов НЭ1 и НЭ2, включенных последовательно с источником ЭДС (рис. 202а). ВАХ нелинейных элементов заданы графически (рис. 202б).

Уравнения Кирхгофа для схемы: U1 + U2=E; I1 =I2 =I.
В соответствии с уравнениями производится сложение ВАХ отдельных элементов U1(I)и U2(I)по оси напряжений (последовательно), в результате чего получается ВАХ для всей схемы U(I). На этой характеристике для значения U=E определяется положение рабочей точки n. Последовательность графического решения показана на рис. 202б стрелками.
Пусть нелинейная цепь состоит из двух нелинейных элементов НЭ1 и НЭ2, включенных параллельно с источником ЭДС E (рис. 203а). ВАХ нелинейных элементов заданы графически (рис. 203б).

Уравнения Кирхгофа для схемы: I1 + I2 = I; U1 = U2 = E.
В соответствии с уравнениями производится сложение ВАХ отдельных элементов I1(U) и I2(U) по оси токов (параллельно), в результате чего получается ВАХ для всей схемы I(U) . На этой характеристике для заданного значения U=E определяется положение рабочей точки n. Последовательность графического решения показано на рис. 203б стрелками.
Пусть нелинейная цепь состоит из двух нелинейных элементов НЭ1 и НЭ2 и линейного резистора R3, включенных по смешанной схеме (рис. 204а). ВАХ нелинейных элементов заданы графически (рис. 204б), а резистор – своим сопротивлением R3. Диаграмма ВАХ для линейного резистора строится в той же системе координат согласно уравнению закона Ома U3 =I3 ×R3

Уравнения Кирхгофа для схемы:

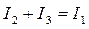 (1)
(1)
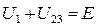 (2)
(2)
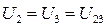 (3)
(3)
Графическое решение задачи выполняется в два этапа. На 1-ом первом этапе проводится сложение ВАХ I2(U2) и I3(U3) по оси токов (параллельно), в результате этого сложения получается ВАХ для параллельного участка схемы U23(I1). На 2-ом этапе проводится сложение ВАХ U1(I1) и U23(I1) по оси напряжений (последовательно), в результате чего получается ВАХ для всей схемы I(U). На этой характеристике для U=Е определяется положение рабочей точки n. Дальнейшая последовательность графического решения показана на рис. 204б стрелками.
Дата добавления: 2020-07-18; просмотров: 701;











