С несколькими источниками ЭДС
Графический метод расчета можно применять также и для более сложных схем с несколькими источниками ЭДС. Последовательность графических операций при решении одной и той же задачи может быть различной и зависит от выбора алгоритма решения.
 Выделим из схемы цепи ветвь, содержащую источник ЭДС Е и нелинейный элемент с заданной ВАХ U(I) (рис. 205 а).
Выделим из схемы цепи ветвь, содержащую источник ЭДС Е и нелинейный элемент с заданной ВАХ U(I) (рис. 205 а).
Из уравнения 2-го закона Кирхгофа следует: 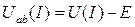 .
.
В той же системе координат U-I построим новую диаграмму ВАХ Uаb(I) путем смещения заданной ВАХ U(I)по оси U на величину (-Е) согласно уравнению 2-го закона Кирхгофа (рис. 206). Можно утверждать, что новая ВАХ Uab(I)соответствует некоторому новому нелинейному элементуНЭЭ, не содержащему ЭДС (рис. 8б). Таким образом, ветвь схемы, содержащую источник ЭДС Е и резистивный (линейный или нелинейный) элемент, можно заменить путем параллельного переноса ВАХ U(I)заданного элемента на величину ЭДС 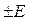 некоторой новой ветвью без источника ЭДС с ВАХ Uab(I)(рис. 205б).
некоторой новой ветвью без источника ЭДС с ВАХ Uab(I)(рис. 205б).

Если в схеме содержится ветвь с источником тока J, то такая ветвь может быть объединена с резистивной ветвью и заменена некоторой эквивалентной, при этом смещение ВАХ элемента производится по оси I на величину 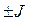 согласно 1-му закону Кирхгофа для узла.
согласно 1-му закону Кирхгофа для узла.
Пусть требуется выполнить расчет схемы (рис. 10а), в которой нелинейные элементы НЭ1 и НЭ2 заданы своими ВАХ, а линейный резистор - сопротивлением R3 ( рис. 10а).
Рассмотрим 2 варианта решения данной задачи.
 1-ый вариант – метод свертки схемы к одному из источников ЭДС, например Е1. Для этого заменим ветвь 2, содержащую нелинейный элемент НЭ2 и ЭДС Е2, новой эквивалентной ветвью с элементом НЭЭ, но без источника ЭДС. После такой замены сложная схема превращается в простую со смешанным соединением элементов (рис. 207б). Графический метод расчета такой схемы был рассмотрен в предыдущем параграфе.
1-ый вариант – метод свертки схемы к одному из источников ЭДС, например Е1. Для этого заменим ветвь 2, содержащую нелинейный элемент НЭ2 и ЭДС Е2, новой эквивалентной ветвью с элементом НЭЭ, но без источника ЭДС. После такой замены сложная схема превращается в простую со смешанным соединением элементов (рис. 207б). Графический метод расчета такой схемы был рассмотрен в предыдущем параграфе.
2-й вариант решения – метод двух узлов. Зададимся положительными направлениями токов во всех ветвях схемы от узла а к узлу b (рис. 207а). Для каждой ветви по 2-му закону Кирхгофа запишем выражения для узлового напряжения:

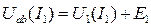 (1)
(1)
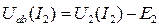 (2)
(2)
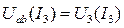 (3)
(3)
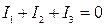 (4)
(4)
Графическое решение задачи производится в соответствии с полученными уравнениями в следующей последовательности:
1) строится диаграмма ВАХ Uab(I1) путем смещения заданной ВАХ U1(I1) по оси U на величину +Е1 согласно уравнению (1) (рис. 208);
2) cтроится диаграмма ВАХ Uab(I2)путем смещения заданной ВАХ U2(I2) по оси U на величину –Е2 согласно уравнению (2) (рис. 208);
3) диаграмма ВАХ Uab(I3)совпадает с заданной U3(I3) согласно уравнению (3) (рис. 208);
4) производится графическое сложение диаграмм ВАХ отдельных ветвей Uab(I1), Uab(I2), Uab(I3) по оси I согласно уравнению (4), в результате чего получается диаграмма результирующей ВАХ 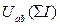 (жирная линия на рис. 208).
(жирная линия на рис. 208).
Рабочая точка n удовлетворяет уравнению (4) 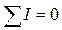 , что соответствует точке пересечения диаграммы результирующей ВАХ
, что соответствует точке пересечения диаграммы результирующей ВАХ 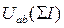 с осью U. Последовательность дальнейшего графического решения показана на рис. 208 стрелками.
с осью U. Последовательность дальнейшего графического решения показана на рис. 208 стрелками.

Дата добавления: 2020-07-18; просмотров: 728;











