Т2. Нелинейные магнитные цепи постоянного потока

Основные понятия и законы магнитной цепи

Электромагнитное поле, которое лежит в основе всех многообразных яв­лений и про­цессов, исследуемых в электротехнике, имеет две равнозначные стороны – электрическую и магнитную. Как известно, в электрической цепи под воздействием источников энергии воз­никают электрические токи, которые про­текают по электрическим проводам. Подобно элек­трическим цепям существуют также магнитные цепи, состоящие из магнитных проводов или кратко магнито­проводов, в которых под воздействием магнитодвижущих сил (МДС) возни­кают и замыкаются магнитные потоки Ф. Формальную схожесть или аналогию между элек­трическими и магнитными цепями в дальнейшем будем именовать принципом двойственно­сти. Следует помнить, что при формальной схожести электрические и магнитные явления физически различны.

Магнитные цепи применяются в электрических машинах, трансформато­рах, электро­магнитных аппаратах, реле, приборах и т.д. Их назначением явля­ется создание заданной ве­личины и формы магнитного потока Ф(t) и проведе­ние его по заданному пути.

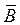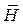Как известно, магнитное поле характеризуется векторными величинами и , ме­жду которыми существует связь 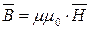, где 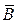- вектор индук­ции (или плотности) маг­нитного поля [Тл], 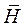- вектор напряженности магнит­ного поля [А/м], который создается электриче­ским током и является первопри­чиной магнитного поля, 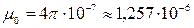[Гн/м] - магнитная проницае­мость пустоты, 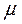- относительная магнитная проницаемость, характеризую­щая спо­собность материала к намагничиванию.

Все материалы по способности их к намагничиванию условно разделяют на две группы: ферромагнитные и неферромагнитные. Для ферромагнитных ма­териалов 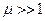. К ним относятся железо (Fe), никель (Ni), кобальт (Co) и их сплавы. Ферромагнитные мате­риалы способны к намагничиванию и создают малое магнитное сопротивление для магнит­ного потока, поэтому применяются в технике для изготовления магнитопроводов. Для не­ферромагнитных материа­лов 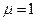, они создают большое сопротивление магнитному потоку и в магнит­ной цепи выполняют роль магнитных изоляторов.

Следует отметить, что если в электрической цепи соотношение между удельной про­водимостью металла (провода) и диэлектрика (изоляция) состав­ляет 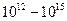, то для маг­нитной цепи это соотношение составляет всего около 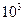. Это означает, что изоляция в маг­нитных цепях очень несовершенна, что в таких цепях существенная часть магнитного потока рассеивается, т.е. замыка­ется через участки с несовершенной магнитной изоляцией.

Зависимость между векторам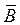и и 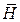для ферромагнитных материалов не имеет точ­ного аналитического выражения, на графической диаграмме эта за­висимость B=f(H), имеет форму петли и называется петлей гистерезиса (рис. 216).

При периодическом перемагничивании материала с увеличением ампли­туды индук­ции B_m площадь петли гистерезиса увеличивается, а ее вершина все больше смещается в об­ласть насыщения материала. Кривая, проходящая через вершины симметричных петель гис­терезиса, называется основной кривой на­магничивания B=f(H)для данного материала. Све­дения об основных кривых намагничивания B=f(H)для ферромагнитных материалов, кото­рые применяются в технике для изготовления магнитопроводов, приводятся в справочной литера­туре в виде таблиц или графических диаграмм и используются в инженерной практике для расчета магнитных цепей.

Пусть требуется выполнить расчет магнитной цепи электромагнитного реле, состоя­щей из катушки с w витками, ярма (неподвижная часть магнитопро­вода), якоря (подвижная часть магнитопровода) и воздушного зазора между яр­мом и якорем (рис. 217а). Геометрические размеры магнитной цепи заданы.

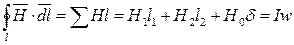
В основе расчета магнитных цепей лежит известный из физики закон полного тока:

.

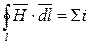При применении закона полного тока к магнитной цепи ее разбивают на отдельные однородные участки, для которых H=const, а контур интегрирования выбирают вдоль маг­нитных линий. При выполнении этих условий интеграл по замкнутому контуру заменяется суммой простых произведений 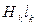, а 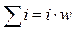. Для рассматриваемого примера получим:

Здесь произведение 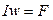называется магнитодвижущей силой (МДС) или намагни­чивающей силой (НС), является источником магнитного потока Ф.

Слагаемые типа H_k·l_k называются магнитным напряжением: 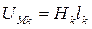[A], а получен­ное выше уравнение представляет собой второй закон Кирхгофа для магнитной цепи:

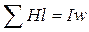или .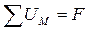

Из курса физики известно, что магнитные линии поля непрерывны. Из этого следует, что магнитный поток Ф на всех участках неразветвленной маг­нитной цепи имеем одно и то же значение 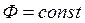. Индукция поля 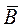и на­пряженность поля 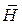на отдельных участках будут различны:

; ; ;

; ; .

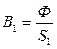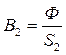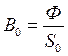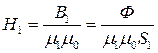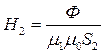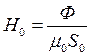Сделаем подстановку в уравнение 2-го закона Кирхгофа:

.

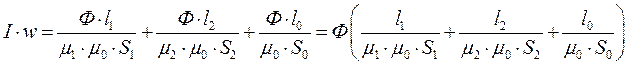Здесь 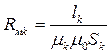- магнитное сопротивление к-го участка магнитной цепи. Для сравнения: формула электрического сопротивления проводника имеет аналогичную струк­туру: 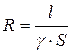, т.е. в магнитной цепи электрической проводимости 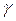соответствует магнит­ная проницаемости материала 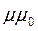. Магнитные сопротивления для участков магнитопровода зависят от магнитной проницаемости 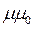, которая является функцией магнитного состояния ( 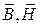). Следовательно, магнитные сопротивления отдельных участков магнитопровода яв­ляются нелинейными и на схеме представляются нелинейными элементами. Магнитное со­противление зазора 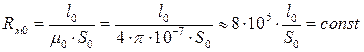и, следовательно, является линейным элементом. С учетом сказанного выше, рассматриваемая магнитная цепь может быть представлена эквивалентной схе­мой с нелинейными элементами (рис. 217б).

Для сложных магнитных цепей, имеющих разветвления и содержащих несколько ис­точников МДС, в полной мере соблюдаются оба закона Кирхгофа:

1)1-й закон Кирхгофа: 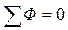- алгебраическая сумма магнитных пото­ков в узле маг­нитной цепи равна нулю;

2) 2-й закон Кирхгофа: 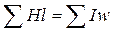- алгебраическая сумма падений магнитных на­пряжений в замкнутом контуре магнитной цепи равна алгебраиче­ская сумма МДС.

Магнитные цепи постоянного потока относятся к классу нелинейных це­пей. В силу принципа двойственности к их расчету применимы все методы рас­чета нелинейных электри­ческих цепей постоянного тока.

Следует отметить, что магнитные цепи обладают своими характерными особенно­стями, которые вносят некоторые отличия в методы их расчета.

2. Аппроксимация вебер-амперных характеристик U_м=f(Ф)нелинейных элементов магнитных цепей

Как было уже сказано, в справочной литературе для каждого типа ферро­магнитного материала, применяемого для изготовления магнитопроводов, при­водятся сведения об ос­новной кривой намагничивания B=f(H) в виде таблицы координат точек или в виде графиче­ской диаграммы этой функции (рис. 218).

Вебер-амперные характеристики (ВАХ) U_м=f(Ф)отдельных однородных участков маг­нитной цепи рассчитывается через их геометрические размеры по основной кривой намагни­чивания: 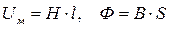. Вследствие пропор­циональной зависимост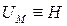и и 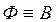графические диаграммы ВАХ от­дельных участков магнитной цепи будут в некотором линей­ном масштабе по­добны диаграмме основной кривой намагничивания B=f(H)(рис. 218).

В аналитических методах расчета магнитных цепей применяется аппрок­симация U_м=f(Ф)для отдельных участков. Рассмотрим эту процедуру на при­мере аппроксимации ос­новной кривой намагничивания B=f(H)(рис. 218).

Для аппроксимации ВАХ, симметричных относительно начала координат, используют нечетные математические функции, например, степенной полином с нечетными степенями или уравнение гиперболического синуса:

.

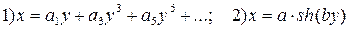Выберем для аппроксимации основной кривой намагничивания степенной полином усеченного вида: 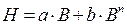. Коэффициенты аппроксимации a, b, n можно определить по методу выбранных точек. Для этой цели на графической диаграмме (или в таблице коор­динат) функции B=f(H) выбираются три точки 1, 2, 3 (по числу определяемых коэффициен­тов), как показано на рис. 3. и опреде­ляются их координаты, например: 1(1,0 Тл, 100 А/м), 2(1,4 Тл, 500А/м), 3(1,5 Тл, 800 А/м). Так как функция B=f(H)в области насыщения описыва­ется в ос­новном вторым слагаемым bBⁿ, то для точек 2 и 3 можно приближенно при­нять:

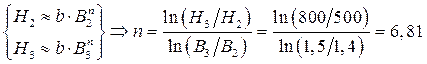
Так как показатель степени n должен быть целым нечетным числом, то принимаем n=7.

Коэффициенты a и b определяются из совместного решения системы уравнений для то­чек 1 и 2:

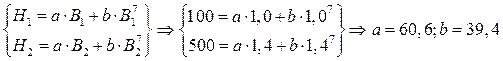
Уравнение аппроксимации примет окончательный вид:

.

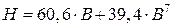При аппроксимации основной кривой намагничивания уравнением гипер­болического синуса 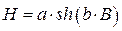коэффициенты аппроксимации определя­ются также по методу вы­бранных точек. Используем для этой цели координаты точек 1 и 2:

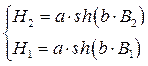
Совместное решение этих уравнений позволяет определить коэффици­енты a и b:

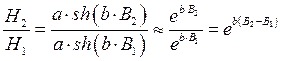, откуда следует

; .

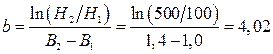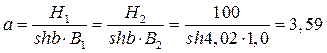Уравнение аппроксимации примет окончательный вид:

.

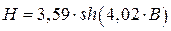Уравнения аппроксимации используются в аналитических методах рас­чета магнитных цепей.