Синтез двухполюсника методом разложения входной функции на простейшие составляющие

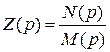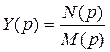Выражение для входной функции или мате­матически можно разложить на простые слагаемые по форме:

.

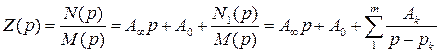Первые два слагаемые выделяют из входной функции 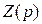путем деле­ния N(p) на М(p) как многочлен на многочлен с целью понижения показателя числителя до значения n=m-1, в результате получают частное 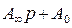и неко­торый остаток N₁(p). Остаток функ­ции раскладывают на простые слагаемые по известной в математике формуле разложения:

,

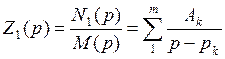где р₁, р₂, …p_m – корни уравнения М(p)=0, 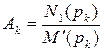- коэффициенты, опре­деляемые со­гласно формуле разложения.

После разложения входной функции на простые слагаемые каждому сла­гаемому подбирают соответствующий ему участок операторной схемы, отдель­ные участки соеди­няют между собой последовательно для функции 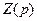или параллельно для функции 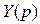, и таким образом получают схему цепи, соот­ветствующей входной функци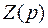и или .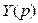

Рассмотрим простейшие схемы соединения элементов и соответствующие им опера­торные изображения.

Þ ;

Þ ;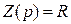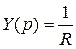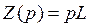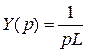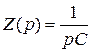

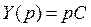
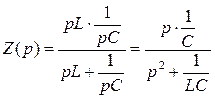
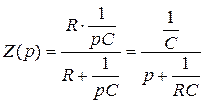
Þ ;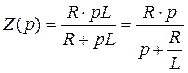

Þ

Þ

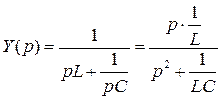
Þ

Þ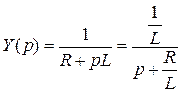

Þ

Þ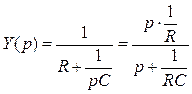

Рассмотрим, каким образом может быть реализовано каждое слагаемое входной функции Z(p). Первому слагаемому 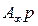соответствует катушка индук­тивности 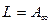, так как 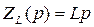. Второму слагаемому 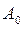соответствует резистор .

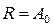Если среди корней р_к имеется корень 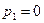, то его подстановка в формулу разложе­ния дает выражение вида 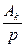, которое в схеме может быть реализовано конденсатором 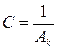, так как .

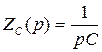Если среди корней р_к имеются мнимые сопряженные корн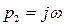и и 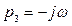, то их подстановка в формулу разложения дает следующее выражение ( ):

,

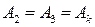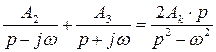которому соответствует параллельный резонансный контур, состоящий из эле­ментов L и С, для которого 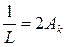и .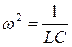

Если среди корней р_к имеется вещественный отрицательный корень 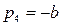, то его подстановка в формулу разложения дает выражение вида 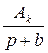, которое может быть реали­зовано схемой с параллельным соединением элемен­тов R и С при соотношени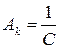и , и .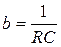

Слагаемые, соответствующие комплексно сопряженным корням 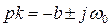, могут быть реализованы более сложными методами, рассмотре­ние которых здесь не приводится.