Характеристика задач синтеза

Синтезом электрической цепи называют определение структуры цепи и пара­метров составляющих ее элементов R, L и С по известным свойствам (характе­ристикам), которым должна удовлетворять цепь. Задачи синтеза цепей проти­воположны по цели и содержанию задачам анализа. В отличие от задач анализа, имеющих, как правило, единственное реше­ние, задачи синтеза могут иметь не­сколько решений, удовлетворяющих заданным условиям. В этом случае выби­рают наиболее рациональное решение (например, по стоимости, по га­баритам, по массе, по числу элементов и т. д.) Кроме того, физического решения может не существовать вообще, так как из существующих реальных элементов не все­гда можно по­строить электрическую цепь, удовлетворяющую заданным усло­виям.

Пусть требуется синтезировать электрическую цепь, для которой заданы вре­менные характеристики на входе: 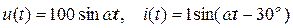. Ком­плексное сопротивление и комплексная проводимость такой цепи равны:

,

.

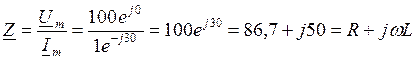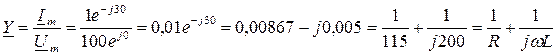Полученным значениям для Z и Y соответствуют две различные схемы за­мещения цепи (рис. 195а, б):

Пусть временные характеристики цепи на входе имеют вид: 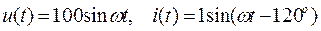. Комплексное сопротивление такой цепи равно:

.

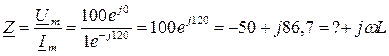Данная цепь на основе пассивных элементовR, L и С физически нереали­зуема, так как в природе не существует резисторов с отрицательным сопротив­лением.

С задачами синтеза на практике встречаются при проектировании слож­ных фильт­ров, корректирующих устройств в радиотехнике, технике связи, ав­томатике и телемеханике.

Синтез электрических цепей развивался по нескольким направлениям:

1) синтез цепи, заданной операторной входной характеристикой;

2) синтез цепи, заданной временной характеристикой в виде реакции цепи на воз­действие импульса напряжения или тока прямоугольной формы, и др.

Наиболее простые результаты получены по первому направлению, кото­рое и будет в дальнейшем рассмотрено.

2. Свойства входных операторных функций пассивных электрических це­пей

Входной функцией цепи (двухполюсника) называется входное оператор­ное сопро­тивление 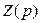или входная операторная проводимость 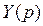. Пусть задана операторная схема некоторой цепи (рис. 196):

Входное операторное сопротивление схемы будет равно:

.

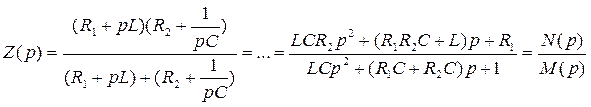Таким образом, входное операторное сопротивление 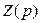или входную операторную проводимость 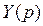для любой схемы можно представить в виде отношения двух полино­мов:

.

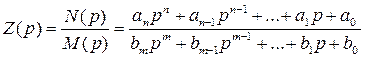Входные операторные функции обладают следующими свойствами:

1)все коэффициенты а_к и b_к в числителе и знаменателе выражения Z(p) должны быть вещественными и положительными числами, так как они образу­ются суммами, произ­ведениями и частными от вещественных параметров эле­ментов R, L и С;

2)наивысшая степень числителя должна отличаться от наивысшей сте­пени знаме­нателя не более, чем на 1;

3)нули и полюсы функции Z(p) должны иметь отрицательную вещест­венную часть;

4)при замене оператора Лапласа на оператор Фурье 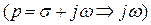веществен­ная часть функции должна быть положительной: .

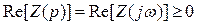Нулями функции Z(p) называются корни р_к уравнения N(p)=0, при под­становке ко­торых значение функции равно нулю: Z(p_к) =0. Полюсами функции Z(p) называются корни р_к уравнения М(p)=0, при подстановке которых значе­ние функции равно бесконечности: Z(p_к) = 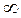. Известно, что свободные состав­ляющие переходного процесса в электрической цепи описываются слагаемыми вида 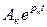и обязательно должны затухать во времени, что возможно только, если действительная часть корней р_к отрицательна.

При замене оператора Лапласа на оператор Фурье 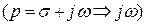оператор­ное сопротивление Z(p) превращается в комплексное сопротивление Z(jw)=R+jX, вещественная часть которого равна активному сопротивлению R, которое не может быть отрицательным.

Функции, обладающие перечисленными свойствами, называются положи­тельными вещественными функциями. Только такие функции могут быть реа­лизованы в виде кон­кретной электрической цепи.