Синтез двухполюсника лестничной (цепной) схемой

Непрерывной дробью называется математическое уравнение вида:

.

Пусть электрическая цепь имеет лестничную (цепную) схему (рис. 197).

Методом свертки выразим входное сопротивление и входную проводи­мость цепной схемы:

Входное сопротивление и входная проводимость цепной схемы выража­ется уравне­нием, которое имеет структурную форму непрерывной дроби.

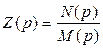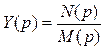Таким образом, задача синтеза двухполюсника, заданного входной функ­цией или , сводится к преобразованию этой функции к виду непре­рывной дроби и последующему переходу к соответствующей этой дроби цепной схеме.

В математике разработаны способы преобразования простых дробей к виду непре­рывной дроби. Порядок такого преобразования показан на конкрет­ном примере:

По аналогичной форме выполняется преобразование к виду непрерывной дроби вы­ражений входных функци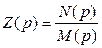й или 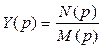. Процесс преобразования можно представить следующим образом:

1) располагают полиномы N(p) и М(p) либо по убывающим, либо по воз­растающим степеням р;

2) делят N(p) на М(p) как многочлен на многочлен, в результате получают частное Ч₁(p) и некоторый остаток О₁(p);

3) делят М(p) на остаток О₁(p) как многочлен на многочлен, в результате получают частное Ч₂(p) и некоторый остаток О₂(p);

4) и т. д. продолжают процесс деления до получения частного без ос­татка;

5) в соответствии с полученной непрерывной дробью составляют цепную схему за­мещения в операторной форме;

6) переходят к физическим параметрам элементов схемы (к электриче­ской схеме) на основе формул соответствия: .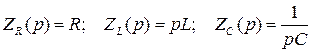

На основании изложенного процесс последовательного деления можно представить следующей схемой:

выходные величины

При делении многочлена на многочлен следят за тем, чтобы в процессе деления в ча­стном содержались только положительные члены, и чтобы они не содержали множитель р в степени больше 1.