Переходные процессы в линии с распределенными параметрами
В цепях с сосредоточенными параметрами переходные процессы протекают одновременно во всех направлениях цепи с одинаковой скоростью затухания.
В цепях с распределенными параметрами переходной процесс, начавшийся в какой-либо точке цепи, распространяется на остальные элементы в виде волн, которые распространяются вдоль цепи с конечной скоростью v. Эта скорость близка к скорости света  км/c в воздушных линиях и v<c для кабельных линий. По мере распространения вдоль линии волна изменяет свою форму, поэтому переходной процесс в разных точках линии выглядит по-разному. Таким образом, переходной процесс в цепи с распределенными параметрами протекает в функции двух переменных – пространства и время.
км/c в воздушных линиях и v<c для кабельных линий. По мере распространения вдоль линии волна изменяет свою форму, поэтому переходной процесс в разных точках линии выглядит по-разному. Таким образом, переходной процесс в цепи с распределенными параметрами протекает в функции двух переменных – пространства и время.
В высоковольтных линиях электропередачи переходные процессы возникают при различных коммутациях, а так же от грозовых явлений в атмосфере. При переходом процессе на отдельных участках линии могут возникнуть перенапряжения, нередко приводящие к пробою изоляции, или большие токи, вызывающие механические разрушения конструкций. Умение рассчитывать эти перенапряжения и сверхтоки необходимы в инженерной практике для правильного выбора и расчета отдельных частей электроустановок.
Анализ переходных процессов в линии с распределёнными параметрами проводится на основе решения ее дифференциальных уравнений, полученных ранее:

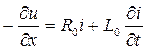
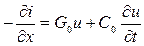 .
.
Решение дифференциальных уравнений в частных производных в общем случае представляет сложную математическую задачу, решение которой выходит за рамки учебного курса ТОЭ. Поэтому здесь ограничимся рассмотрением частного случая линии без потерь, т.е. при условии 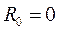 ,
, 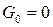 .
.
Дифференциальные уравнения линии без потерь получат вид:

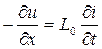 ;
;
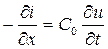 .
.
Выполним решение этой системы дифференциальных уравнений, для чего каждое из уравнений продифференцируем сначала по переменной х, а потом по переменной t:




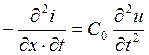
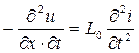
Совместное решение каждой пары полученных уравнений дает результат:

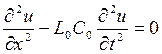
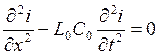
Введем обозначение 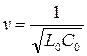 - скорость волны, после чего уравнения примут вид:
- скорость волны, после чего уравнения примут вид:

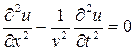
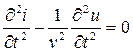
В курсе математики уравнения данного вида получили название волновых, и им соответствует следующие решения (без вывода):
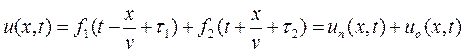 ,
,
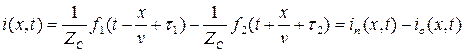 .
.
Дата добавления: 2020-07-18; просмотров: 550;











