Линия с распределенными параметрами без потерь

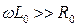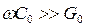Для кабельных линий с распределенными параметрами, работающих на высоких час­тотах (линии связи), реактивные параметры значительно превосхо­дят активные и . При расчете режимов таких линий можно без особого ущерба для точности рас­чета пренебречь активными параметрами и принять их равными нулю 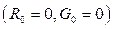. В таком случае линия становится идеальной или без потерь.

Волновое сопротивление линии без потерь:

-

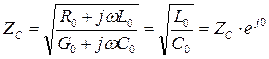является чисто активным и не зависит от частоты.

Постоянная распространения линии без потерь:

,

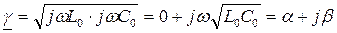где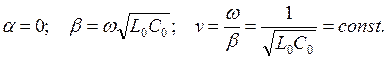

В линии без потерь отсутствует затухание сигнала 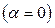, а фазовая ско­рость v не зависит от частоты, следовательно, линия без потерь является неис­кажающей.

Учитывая математические соотношения, что 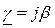, и

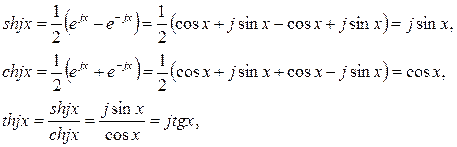
преобразуем комплексные уравнения установившегося синусоидального режима ли­нии:

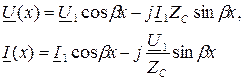- при отсчете координаты х от начала линии,

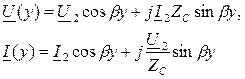- при отсчете координаты y от конца ли­нии,

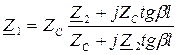- входное сопротивление линии.

Режим линии без потерь определяется свойствами (параметрами) самой линии и ве­личиной и характером нагрузки 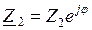на ее конце. Исследуем работу линии в различ­ных режимах нагрузки.

1.Режим согласованной нагрузки: .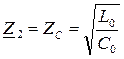

Учитывая, что 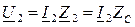, комплексные уравнения линии получат следую­щий вид:

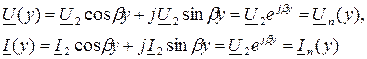- при отсчете координаты y от конца линии,

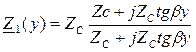- входное сопротивление линии.

В режим согласованной нагрузки напряжение u(t,y) и ток i(t,y) состоят только из па­дающих волн, которые распространяются от начала линии к ее концу без затухания. Дейст­вующие значения напряжения U(y) и тока I(y) не за­висят от координаты у и во всех точках линии имеют одинаковые значения.

Входное сопротивление линии 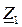равно волновому 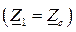и не зависит от длины линии. Графические диаграммы названных функций пока­заны на рис. 181

2.Режим холостого хода: 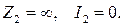Комплексные уравнения ре­жима линии получат вид:

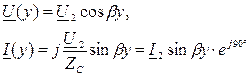- при отсчете координаты y от конца ли­нии,

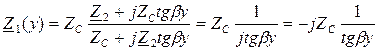- входное сопротивление ли­нии.

Входное сопротивление линии Z₁(у), является чисто реактивным, его ве­личина и ха­рактер зависят от длины линии.

Графические диаграммы названных функций показаны на рис. 2.

Режим линии, при котором в некоторых ее точках наблюдаются макси­мальные зна­чения напряжения (тока) или пучности, а в других ее точках – ну­левые значения этих вели­чин или узлы, получил название в технике режима стоячих волн. Узлы и пучности для од­ной и той же величины следуют друг за другом через отрезки равны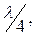е где 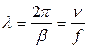- длина волны, при этом узлы одной величины совпадают с пучностями другой.

Режим стоячих волн физически можно объяснить как результат наложе­ния падаю­щей и наложенной волн с одинаковыми амплитудами. В точках ли­нии, в которых мгновен­ные значения падающей и отраженной волн всегда сов­падают, образуются пучности, а в точках, где эти значения складываются с про­тивоположным знаком (в противофазе), обра­зуются узлы.

Следует отметить, что режим стоячих волн имеет место в линии без по­терь при чисто реактивной нагрузке 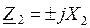любой величины ( 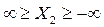). При реактивной нагрузке энергия, доставляемая падающей вол­ной в конец линии, полностью отражается, при этом амплитуда отраженной волны равна амплитуде подающей волны. Входное сопротивление линии при реактивной нагрузке 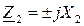является чисто реактивным:

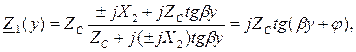где .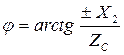

3.Режим произвольной нагрузки: .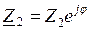

Расчет режима линии производится путем совместного решения ее ком­плексных уравнений и уравнений закона Ома: 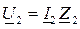и 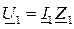. При произ­вольной несогласован­ной нагрузке в конце линии происходит частичное отра­жение волн, при этом амплитуды отраженных волн напряжения и тока будут меньше амплитуд падающих волн. Распределе­ние действующих значений на­пряжения и тока вдоль линии будет носить волнообразный характер рис. 3, при этом максимумы и минимумы функции будут следовать друг за другом через интервал .

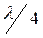Степень несогласованности сопротивления нагрузки 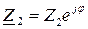с волно­вым сопро­тивлением линии Z_C характеризуется коэффициентом стоячей волны:

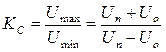
В реальных условиях для согласования нагрузки с линией применяются специальные согласующие устройства.