Решение второго нелинейного уравнения

Для решения второго по заданию нелинейного уравнения, например, вида 3sin(x/2) = 2x² - 4, необходимо выполнить следующие действия:

– выделить на листе Excel диапазон ячеек, в которых решалось первое уравнение, то есть в данной адресации A1:T38;

– скопировать выделенный фрагмент, например, со строки 42, как показано на рис. 2.4.1;

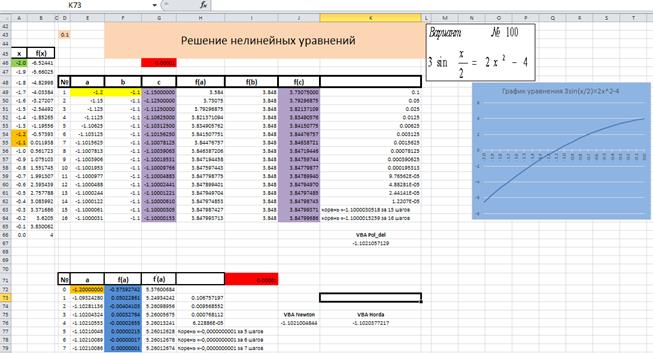
Рис. 2.4.1

– создать модули VBA для нового уравнения, в данном случае, 3sin(x/2) = 2x² – 4:

Function nel_ur_2(x)

nel_ur_2 = 3 * Sin(x / 2) - 2 * x ^ 2 + 4

End Function

Function nel_ur_2D(x)

nel_ur_2D = 3 * Cos(x / 2) + 1 / 2 - 2 * x

End Function

Function Pol_del2(a As Double, b As Double, e As Double)

Dim c As Double

10 c = (a + b) / 2

If nel_ur_2(a) * nel_ur_2(c) < 0 Then b = c Else a = c

If Abs(a - b) <= e Then Pol_del2 = Format(c, "0.0000000000") Else GoTo 10

End Function

Function Newton2(a As Double, e As Double)

x = a

x1 = x - nel_ur_2(x) / nel_ur_2D(x)

While Abs(x - x1) > e

x = x1

x1 = x - nel_ur_2(x) / nel_ur_2D(x)

Wend

Newton2 = Format(x1, "0.0000000000")

End Function

Public Function Horda2(a As Double, b As Double, delta As Double)

Dim c1 As Double, c2 As Double, Fa As Double, Fb As Double, Fc As Double

Fa = nel_ur_2(a)

Fb = nel_ur_2(b)

If Fa * Fb > 0 Then

MsgBox ("Интервал [a, b] выбран неправильно")

Exit Function

End If

Do

c2 = c1

c1 = a - (b - a) / (Fb - Fa) * Fa

Fc = nel_ur_2(c)

If Fc * Fa > 0 Then b = c1: Fb = Fc Else a = c1: Fa = Fc

Loop Until Abs(c1 - c2) > delta

Horda2 = Format(c1, "0.0000000000")

End Function

– заменить в диапазоне ячеек B46:B66 функцию =nel_ur_1 на функцию =nel_ur_2, рис. 2.4.1;

– подобрав значения ячеек A46и D43, выполнить этап отделения корней для второго уравнения, то есть для функции nel_ur_2, в данном случае ячейками, в которых функция nel_ur_2 меняет знак, являются ячейки A54 и A55;

– скопировать значение ячейки A54 в ячейку E49, то есть записать E49= A54;

– скопировать значение ячейки A55 в ячейку F49, то есть записать F49= A55;

– заменить в диапазоне ячеек H49:J64 функцию =nel_ur_1 на функцию =nel_ur_2, рис. 2.4.1;

– в ячейке K63 в данной адресации появится сообщение корень = -1.1000030518 за 15 шагов (для решаемого варианта задания).

Таким образом, нелинейное уравнение 3sin(x/2) = 2x² – 4в среде Excel решено методом дихотомии и корень уравнения равен -1.1000030518.

При этом заданная точность решенияe = 0.00001 достигнута за 15 итераций.

Для решения заданного уравнения в среде VBA необходимо, например в ячейке K67, с помощью мастера функций f_x вызвать модуль Pol_del2.

В появившемся окне Аргументы функции подставить значения ячеек E49, F49 и G46, как показано на рис. 2.4.2 и, нажав кнопку OK, получить результат -1.1021057129.

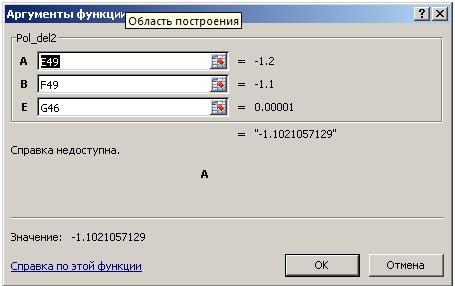
Рис. 2.4.2

Для решения второго по заданию нелинейного уравнения, вида 3sin(x/2) = 2x² - 4, методом Ньютона необходимо выполнить следующие действия:

– скопировать значение ячейки A54 в ячейку E72, то есть записать E72= A54;

– заменить в диапазоне ячеек F72:F79 функцию =nel_ur_1 на функцию =nel_ur_2, рис. 2.4.1;

– заменить в диапазоне ячеек G72:G79 функцию =nel_ur_1D на функцию =nel_ur_2D, рис. 2.4.1;

– в ячейке H77 в данной адресации появится сообщение корень = -1.1021004844 за 5 шагов (для решаемого варианта задания).

Таким образом, нелинейное уравнение 3sin(x/2) = 2x² – 4в среде Excel решено методом Ньютона и корень уравнения равен -1.1021004844.

При этом заданная точность решенияe = 0.00001 достигнута за 15 итераций.

Для решения заданного уравнения в среде VBA необходимо, например, в ячейке J76, с помощью мастера функций f_x вызвать модуль Newton2.

В появившемся окне Аргументы функции подставить значения ячеек E49, F49 и G46, как показано на рис. 2.4.3 и, нажав кнопку OK, получить результат -1.1021004844.

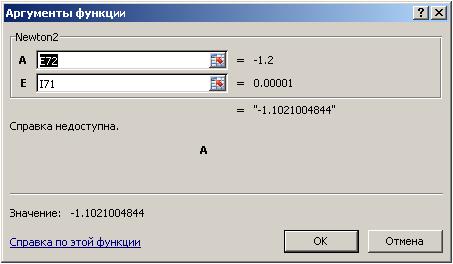
Рис. 2.4.3

Для решения заданного уравнения в среде VBA методом Хорд необходимо, например, в ячейке K76, с помощью мастера функций f_x вызвать модуль Horda2.

В появившемся окне Аргументы функции подставить значения ячеек E49, F49 и G46, как показано на рис. 2.4.4 и, нажав кнопку OK, получить результат -1.1020377217.

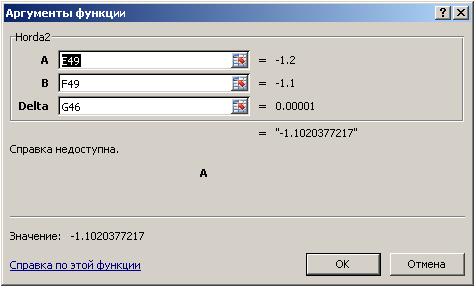
Рис. 2.4.4

Как и при реализации метода дихотомии и метода Ньютона недостатком использования функции VBA является то, что функция возвращает только один параметр и определить количество итераций в данном случае невозможно.

К достоинствам использования функции VBA относится то, что можно изменять значение точности вычислений без построения достаточно объёмной таблицы.