Метод Ньютона (метод касательных)

Графически решение не линейного уравнения методом Ньютона можно проиллюстрировать с помощью рис. 2.2.1.

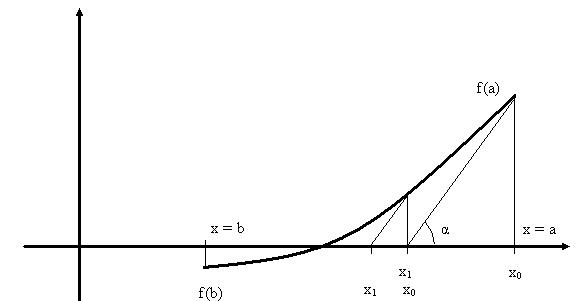
Рис. 2.2.1

К точке f(a) = f(x₀) проводится касательная до пересечения с осью абсцисс в точке x₁. Это первое приближение к корню. Затем вычисляется величина |x₀-x₁|, если |x₀-x₁|<=e,то значение x₁ принимается за корень уравнения, если нет, то процесс повторяется, при этом x₀ = x₁, а x₁ определяется снова.

Так как tgα = f ^’(x₀), то

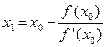(2.2.1)

Алгоритм нахождения корней нелинейного уравнения методом Ньютона с заданной точностью eпредставлен на 2.2.2.

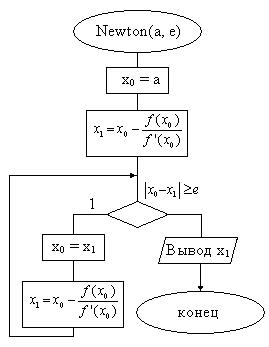
Рис. 2.2.2

Суть алгоритма в следующем:

– в программу, в данном случае, с именем Newton с двумя формальными параметрами a и e, передаётся значение начала (или окончания) промежутка [a;b], в котором обнаружен корень, и значение точности;

– присваивается x₀ = a;

– по формуле, соответствующей 2.2.2, вычисляется x₁;

– вычисляется величина |x₀-x₁|,

– если |x₀-x₁|<e,то значение x₁ принимается за корень уравнения, если нет, то процесс повторяется, при этом присваивается x₀ = x₁, а x₁ определяется снова.

– значение последней точки x₁ и есть корень уравнения с заданной точностью e.

Так как этап отделения корней для заданного варианта уже выполнен, то решение нелинейного уравнения 2x³+x²-3x+2=0методом Ньютона в средеExcel можно начинать с создания “шапки” таблицы, как показано на рис. 2.1.2, строка 30.

Заполнить первую строку таблицы:

– в ячейку E31 записать =A17;

– в ячейке F31 с помощью мастера функций f_x вызвать модуль, соответствующий решаемому уравнению =nel_ur_1(E31);

– убедиться, что значения ячеек F31 и B17 совпадают;

– в ячейке G31 с помощью мастера функций f_x вызвать модуль соответствующий первой производной от функции решаемого уравнения =nel_ur_1D(E31);

Модуль nel_ur_1Dоформить в VBA предварительно: