Метод половинного деления (Дихотомия)

Определение 2.1.1 – корень уравнения это число (или числа), при подстановке которого (которых) в уравнение оно обращается в ноль или тождество.

Любому методу решения нелинейного уравнения предшествует этап отделения корней.

Определение 2.1.2 – отделение корней это установление достаточно тесного промежутка (или промежутков) значений на оси Х, в котором (в которых) находится корень.

Алгоритм нахождения корней нелинейного уравнения методом половинного деления с заданной точностью eпредставлен на 2.1.1.

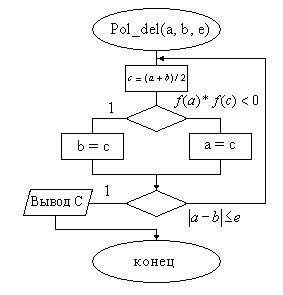
Рис. 2.1.1

Суть алгоритма в следующем:

– в программу, в данном случае, с именем Pol_del с тремя формальными параметрами a, b и e, передаются значения промежутка [a;b], в котором обнаружен корень, и значение точности;

– вычисляется значение средней точки промежутка c=(a+b)/2;

– определяется, в какой половине промежутка функция уравнения f(x) поменяла знак, для чего вычисляется логическое выражение f(a) * f(c)<0;

– если результат вычисления логического выражения равен 1, значит функция уравнения f(x) поменяла знак в первой половине промежутка [a;b] и поэтому b = c, в противном случае a = c;

– процесс повторяется до тех пор, пока не выполнится условие |a-b|<=e;

– значение средней точки последнего промежутка [a;b] и есть корень уравнения с заданной точностью e.

На рис. 2.1.2 приведён пример решения нелинейного уравнения

2x³+x²-3x+2=0.

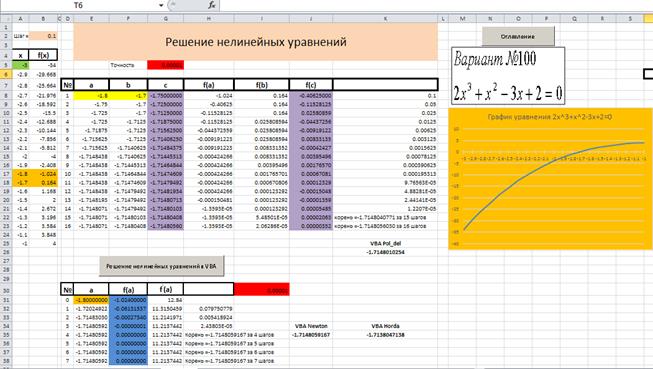
Рис. 2.1.2

Начинать выполнение задания следует с создания в VBA модуля, соответствующего функции уравнения задания, в данном случае это:

Function nel_ur_1(x)

nel_ur_1 = 2 * x ^ 3 + x ^ 2 - 3 * x + 2

End Function

Затем в диапазоне A5:B25, в данной адресации, необходимо получить таблицу значений функции nel_ur_1 от аргумента X. Построить график этой функции.

При этом начальное значение аргумента X, ячейка A5, и начальное значение шага изменения аргумента X, ячейка B2, подбираются таким образом, чтобы на графике чётко увидеть пересечение кривой графика функции с осью абсцисс. Это есть графическое решение заданного нелинейного уравнения.

В таблице, в столбце значений аргументов X, диапазон A5:A25, определить пару значений аргумента X, при которых функция, диапазон B5:B25, меняет знак. В данном случае это пара ячеек A17:A18.

Таких пар может быть несколько.

Этап отделения корней завершён.

Далее в строке 7, оформить “шапку” таблицы, как показано на рис. 2.1.2.

Заполнить первую строку таблицы:

– в ячейку E8 записать =A17;

– в ячейку F8 записать =A18;

– в ячейку G8 записать арифметическое выражение, вычисляющее значение средней точки =(F8+E8)/2;

– в ячейке H8 с помощью мастера функций f_x вызвать модуль, соответствующий решаемому уравнению =nel_ur_1(E8);

– в ячейке I8 с помощью мастера функций f_x вызвать модуль, соответствующий решаемому уравнению =nel_ur_1(F8);

– в ячейке J8 с помощью мастера функций f_x вызвать модуль, соответствующий решаемому уравнению =nel_ur_1(G8);

– убедиться, что значения ячеек B17 и H8 совпадают;

– убедиться, что значения ячеек B18 и I8 совпадают;

– в ячейку F8 записать условный оператор =ЕСЛИ(ABS(E8-F8)<=$G$5;"корень ="&ТЕКСТ(G8;"0.0000000000")&" за "&D8&" шагов";ABS(E8-F8)).

Заполнить вторую строку таблицы:

– в ячейку E9 записать условный оператор =ЕСЛИ(H8*J8<0;E8;G8);

– в ячейку F9 записать условный оператор =ЕСЛИ(H8*J8<0;G8;F8);

– выделить диапазон G8:K8 первой строки таблицы и скопировать на вторую строку таблицы;

– выделить диапазон E9:K9 второй строки таблицы и скопировать вниз до тех пор пока, в столбце K не появится сообщение корень = -1.7148040771 за 15 шагов (для решаемого варианта задания).

Таким образом, нелинейное уравнение 2x³+x²-3x+2=0в среде Excel решено методом дихотомии и корень уравнения равен -1.7148040771.

При этом заданная точность решенияe = 0.00001 достигнута за 15 итераций.

Для решения заданного уравнения в среде VBA необходимо создать модуль VBA: