Структура процесса решения задачи

Учитель должен работать над формированием каждого из перечисленных этапов решения задачи. Рассмотрим реализацию этой схемы на примерах решения некоторых задач.

№1. Катер вышел одновременно с плотом, и прошёл по течению реки 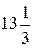км, затем, не останавливаясь, 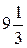км в обратном направлении, где и встретился с плотом. Найдите, во сколько раз собственная скорость катера больше скорости течения.

1. В результате анализа условия задачи может появиться такой рисунок.

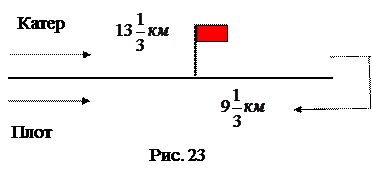
2. Метод: составление уравнения (математического моделирования).

3. Ведем переменную и выразим время, затраченное на весь путь катером и плотом. Учитывая их равенство, составим и решим уравнение.

4. Пусть 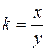, где х км/ч – собственная скорость катера, а у км/ч – скорость течения. Катер по течению проплыл 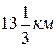со скоростью х+у км/ч за 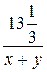ч, а против течения 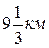со скоростью х - у км/ч за 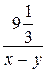ч. На весь путь он затратил 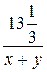+ 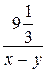. Плот до встречи прошёл 4 км и на весь путь затратил 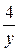км.

Уравнение: 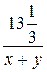+ 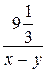= 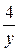. Данное уравнение равносильно уравнению , , ,

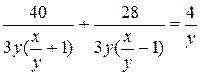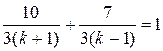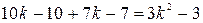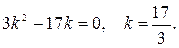
5. Проверку решения предлагаем выполнить самостоятельно.

6. Ответ: отношение скоростей катера и плота 17:3.

7. Анализируя решение, попытаемся найти второй способ.

Вычислим отношение пройденных расстояний: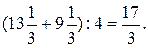

Покажем, что не случайно совпали отношения скоростей и пройденных расстояний. По условию задачи можно составить уравнение 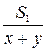+ 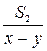= 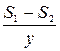, где х км/ч – собственная скорость катера, а у км/ч – скорость плота (скорость течения), S₁ – путь, пройденный катером по течению, S₂ – путь, пройденный катером против течения, а S₁ – S₂ – путь, пройденный плотом. Выполним цепочку преобразований.

Левая часть: 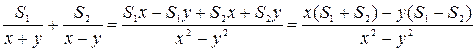. Соединим с правой частью. = ,

= , = ,

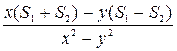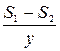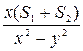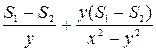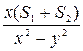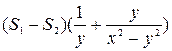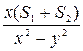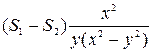= . Следовательно, 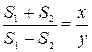. Что и требовалось доказать. Ответ, полученный вторым способом, делает решение простейшим, однако его обоснование достойно первого способа решения.

№2. Длина окружности, описанной около равнобедренного треугольника, равна 20p. Найти площадь этого треугольника, если его основание равно 12.

В результате анализа условия задачи выполняем чертёж и записываем условие и заключение в форме «дано», «доказать».

Дано: DАВС, АВ=ВС, АС=12.

Окружность описана около DАВС,

длиной 20p.

Найти: S_DABC.

Рис. 24

Поиск решения. Чтобы найти площадь данного треугольника, достаточно знать его высоту. По условию задачи легко найти радиус R описанной окружности. Тогда из DАОН по теореме Пифагора вычисляется ОН. Далее считается высота и площадь.

План решения Реализация плана решения.

1. АО=R. 1. 20p=2pR. R=10. АО=ОВ=10.

2. АН. 2. АН=1/2 АС, АН=6.

3. ОН. 3. DАОН:, ОН²=АО²-АН². ОН=8.

4. ВН. 4. ВН=ОН+ОВ, ВН=18.

5. S_DABC._. 5. S_DABC=108.

Проверка убеждает в правильности решения и ответа. Однако исследование задачной ситуации позволяет выявить ещё один случай взаимного расположения треугольника и окружности

Задача имеет ещё одно решение. В этом случае ВН= ОВ-ОН, ВН=2, а S_DABС =12.

Отметим, что важное внимание следует уделять обучению приёмам поиска решения задачи. Некоторые из них (анализ в форме расчленения, нисходящий и восходящий анализ) мы рассмотрим ниже.

Литература

1. Методика и технология обучения математике. Курс лекций: пособие для вузов / под науч. ред. Н.Л. Стефановой. – М., Дрофа, 2005.

2.Саранцев Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / Г. И. Саранцев, - М.: Просвещение, 2002.

3. Методика преподавания математики в средней школе: общая методика, Учеб. пособие для студентов пед. ин-тов / составители Р. С. Черкасов, А. А. Столяр. – М., Просвещение, 1985.