Обобщение и абстрагирование
Обобщение и абстрагирование - два логических приёма, применяемых почти всегда совместно в процессе познания.
Обобщение – мысленное выделение, фиксирование каких либо общих существенных свойств, принадлежащих данному классу объектов или отношений. Абстрагирование - мысленное отвлечение, отделение общих существенных свойств, выделенных в результате обобщения, от прочих несущественных или необщих свойств рассматриваемых предметов или отношений и отбрасывание (в рамках нашего изучения) последних.
Обобщение и абстрагирование применяются как эвристическое средство и как средство введения нового понятия. Приведём примеры.
1. В математике понятие производной вводится посредством двух задач: о скорости и о касательной. Обобщая процесс решения этих задач приходим к выводу, что в каждом случае мы действовали по одному и тому же общему алгоритму: придавали приращение аргументу, находили соответствующее приращение функции, затем вычисляли отношение этих приращений и его предел. Абстрагируясь от конкретного содержания задач, вводим понятие производной
2. В школе проиллюстрируем применение этих методов при изучении распределительного закона умножения относительно сложения в 5 классе.
Учащимся предлагаются следующие задачи.
№1. В школьном саду посажены фруктовые деревья в 8 рядов. В каждом ряду посажено по 7яблонь и 5 груш. Сколько всего деревьев посажено в саду?
Решение.
1 способ. 7+ 5деревьев посажено в каждом ряду, а всего (7+5)×8 деревьев;
2 способ. 7×8 яблонь было посажен в саду, 5×8 – груш, а всего 7×8+5×8 деревьев.
По смыслу задачи ясно, что справедливо равенство (7+5)×8=7×8+5×8.
Ответ: 96 деревьев.
№2. Автобус и автомобиль одновременно выехали навстречу друг другу из двух пунктов. Скорость автобуса 60 км/ч, а автомобиля 80 км/ч. Через три часа они встретились. Каково расстояние между пунктами?

|
|
1 способ. Скорость сближения автобуса и автомобиля (60+80) км/ч, за 3 часа они сблизятся на (60+80)×3 км.
2 способ. Автобус до встречи пройдёт 60×3 км, а автомобиль 80×3 км. Расстояние между пунктами составит (60×3 + 80×3) км.
По смыслу задачи ясно, что справедливо равенство (60+80)×3=60×3+80×3.
Ответ: 420 км.
№3. Найти общую площадь двух участков прямоугольной формы, изображённых на рисунке.

1 способ. Решая задачу, можно составить выражение (5+3) ×4 (кв.м).
2 способ. Решая задачу, можно составить выражение 5×4+3×4 (кв.м).
По смыслу задачи ясно, что справедливо равенство (5+3) ×4=5×4+3×4.
Ответ: 32 кв.м.
Обобщая решения задач и абстрагируясь от их конкретного содержания, приходим к выводу, что для того, чтобы умножить сумму двух чисел на третье число, можно каждое слагаемое умножить на это число и полученные произведения сложить. Запишем этот закон с помощью переменных:
(а + b) × с =а× с + b× с
и назовём его распределительным законом умножения относительно сложения.
Обобщение и абстрагирование могу использоваться при решении задач.
Рассмотрим задачу: для того, чтобы выяснить, сколько рыб в пруду, взяли сеть с заранее выбранным размером ячеек и, вытащив её, обнаружили 30 рыб. Отметили каждую меткой и бросили обратно в пруд. На другой день забросили эту же сеть и поймали 40 рыб, причём среди них две меченные. Сколько рыб в пруду, годных для улова?
Решение. Так как меченные рыбы составляют 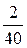 или
или 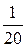 всех рыб, а всего их 30, то рыб в пруду не менее 20×30=600.
всех рыб, а всего их 30, то рыб в пруду не менее 20×30=600.
Обобщая существенные данные задачи и абстрагируясь от её конкретного содержания, сформулируем общую задачу: имеется урна с шарами. Из неё извлекается k шаров и делается пометка. Шары возвращаются в урну и перемешиваются. После этого извлекается п шаров и обнаруживается, что среди них т меченых шаров (т£п). Сколько шаров в урне?
Решая по аналогии с задачей о рыбах, получим, что меченые шары составляют 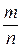 часть или k шаров. Следовательно, шаров в урне
часть или k шаров. Следовательно, шаров в урне 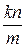 .
.
Анализ и синтез
Анализ и синтез могут рассматриваться в двух формах:
1) анализ - логический приём, состоящий в том, что изучаемый предмет мысленно разбивается на части, каждая из которых затем исследуется отдельно, а синтез как обратная операция восстановления целого (анализ в форме расчленения);
2) анализ - метод рассуждений от искомых к данным задачи, а синтез -от данных к искомым (анализ в форме рассуждения).
Общая схема анализа в форме расчленения:
· разбиваем условие задачи на отдельные части;
· выделяем некоторые условия (остальные пока не учитываются);
· из отобранных условий составляем более лёгкую вспомогательную задачу и решаем её;
· дополняем отброшенные условия и переходим к решению данной задачи.
Примеры.
№1. Сократить дробь 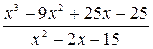 .
.
Естественно разбить данную дробь на числитель и знаменатель. Знаменатель тривиально раскладывается на множители 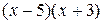 . Проверим, какие из нулей знаменателя х=5 или х=-3 являются нулями числителя. Убеждаемся, что это х=5. Выделяем в числителе множитель х-5:
. Проверим, какие из нулей знаменателя х=5 или х=-3 являются нулями числителя. Убеждаемся, что это х=5. Выделяем в числителе множитель х-5: 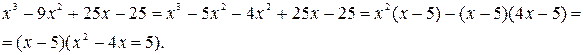
В результате получаем 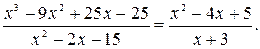
№2. Построить треугольник по отношению т : п двух сторон, углу между ними и высоте проведенной к третьей стороне.
Вычленим условие: построить треугольник по отношению т : п двух сторон, углу между ними. Треугольник со сторонами т и п и с углом между ними, равным данному удовлетворяет выделенным условиям. Построим его.

Подключаем данную по условию высоту, проведённую к третьей стороне. Построим её в полученном треугольнике.

Достроим полученную конфигурацию до искомого треугольника.

|
DМАС – искомый.
Такой приём решения задач иногда называю разбиением на подзадачи.
Примером анализа в форме расчленения является исследование функции по известному плану, а синтеза – построение её графика на основе полученных в процессе анализа свойств.
Анализ в форме рассуждений делится на нисходящий и восходящий.
Нисходящий анализ
Суть нисходящего анализа состоит в следующем. Предполагаем, что утверждение А, которое следует доказать истинно. Подбираем следствие В из него, следствие С из В и так до тех пор, пока не получим истинное утверждение. Проверяем обратимость наших утверждений. Делаем вывод.
Примеры.
№1. Доказать, что если 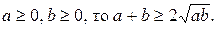
Начинаем с того, что следует доказать, предполагая, что неравенство верно.
 Пусть
Пусть 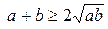 истинно. Подбираем следствие.
истинно. Подбираем следствие.

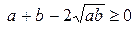 истинно,
истинно,
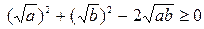 истинно,
истинно,

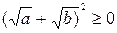 истинно. Проверяем обратимость наших утверждений и делаем вывод, что неравенство доказано.
истинно. Проверяем обратимость наших утверждений и делаем вывод, что неравенство доказано.
№2. Доказать, что в равнобедренной трапеции квадрат диагонали равен квадрату боковой стороны, сложенному с произведением оснований.
 Дано: ABCD – трапеция,
Дано: ABCD – трапеция,
АВ=CD.
Доказать: 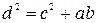 .
.
Нисходящий анализ.
 Пусть
Пусть 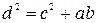 истинно.
истинно.

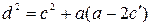 истинно (
истинно ( 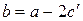 ).
).
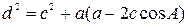 истинно (
истинно ( 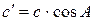 ).
).

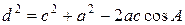 истинно
истинно
(доказанная теорема косинусов).
Все рассуждения обратимы, следовательно, равенство доказано. Отметим, что запись доказательства следует начинать с последней строчки, и тогда придём к утверждению, которое следует доказать.
№3. Доказать, что если 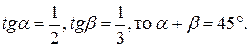
Нисходящий анализ.
 Пусть
Пусть 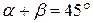 истинно.
истинно.

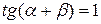 истинно.
истинно.

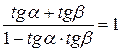 истинно.
истинно.

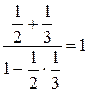 истинно.
истинно.
1=1 истинно.
Однако утверждение нельзя считать доказанным, так как если 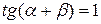 истинно, то из него не следует, что
истинно, то из него не следует, что 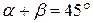 истинно (необратимое рассуждение).
истинно (необратимое рассуждение).
Восходящий анализ
Суть восходящего анализа состоит в следующем. Пусть следует доказать утверждение А. Подбираем утверждение В, из которого следует утверждение А, затем – утверждение С, из которого следует утверждение В и так далее, пока не получим истинное утверждение. Так как В Þ А, то В – достаточное условие А. Поэтому восходящий анализ сопровождается словами «для того, чтобы доказать А достаточно доказать В; для того, чтобы доказать В достаточно доказать С…» Заметим, что проверять обратимость утверждений восходящий анализ не требует.
Примеры.
№1.
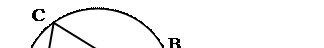 Доказать, что если через точку, взятую внутри круга, проведены две произвольные хорды, то произведение длин отрезков каждой из хорд равны.
Доказать, что если через точку, взятую внутри круга, проведены две произвольные хорды, то произведение длин отрезков каждой из хорд равны.
Дано:
круг,
АВ, CD – хорды,
О – точка пересечения хорд.
|
Восходящий анализ.
 Для того, чтобы доказать равенство АО×ОВ=СО×ОD,
Для того, чтобы доказать равенство АО×ОВ=СО×ОD,
 достаточно доказать
достаточно доказать 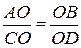 ,
,
достаточно доказать DАОС~DDОВ,

достаточно доказать Ð1=Ð2, Ð3=Ð4 истинно, так как
вертикальные углы равны и
вписанные углы, опирающиеся
на одну и ту же дугу равны.
Запись доказательства следует выполнять с последней строчки.
Ценность анализа и синтеза состоит в том, что они являются средством поиска решения задачи, доказательство теоремы. Используя их, учащиеся могут самостоятельно доказать многие (конечно не все) теоремы самостоятельно. Например, свойства и признаки параллелограмма, прямоугольника, ромба, признак перпендикулярности прямой и плоскости и ряда других.
Индукция и дедукция
Индукцию рассматривают как один из видов умозаключения, как метод исследования, как форму изложения учебного материала. Смысл применения индукции в каждом из названных случаев заключается в словах «от частного к общему».
Примеры.
№1.
Рассмотрим частные суждения:
Окружность, эллипс, парабола, гипербола пересекаются с прямой не более, чем в двух точках.
Окружность, эллипс, парабола, гипербола – кривые второго порядка. Индуктивное умозаключение: все кривые второго порядка могут пересекаться с прямой не более, чем в двух точках. Это истинное утверждение.
№2.
Исследуем значения функции f(n)= n2-n+41 при nÎN.
Заполним таблицу
| n | ||||||||||
| f(n) |
На основании рассмотренных значений можно прийти к выводу, что при лбом натуральном значении п значение данной функции - простое число. Вывод оказывается неверным. Так, при п = 41 f(41)=412-41+41, f(41)=412 – составное число.
В учебниках математики 5-6 классов материал изложен зачастую индуктивно: от частных примеров к общему выводу.
Виды индукции
Индукция бывает полная и неполная. Полная индукция предполагает рассмотрение всех частных случаев. Она является методом доказательства.
Например, теорема об угле, вписанном в в окружность доказывается методом полной индукции для трёх случаев: центр окружности принадлежит стороне угла, лежит между его сторонами, лежит вне угла.



Рис. 37
Методом полной индукции можно доказать, что всякое чётное число большее 2, но меньше 14 можно представить в виде суммы двух простых чисел. Составим их полный список: 4, 6, 8, 10,12. Тогда 4=2+2, 6=3+3, 8=3+5, 10=3+7=5+5, 12= 5+7. Все частные случаи рассмотрены. Утверждение доказано.
Неполная индукция заключается в том, что рассматриваются не все частные случаи. Неполная индукция не есть метод доказательства, однако она является мощным эвристическим средством, с помощью которого, рассматривая частные случаи, учащиеся самостоятельно приходят к общим выводам (верным или неверным). Известно, что индуктивный метод и в науке привёл к ряду гипотез (проблема Гольдбаха, Теорема Ферма).
Дедукция
Дедукция (от латинского deductio – выведение) есть форма умозаключения, при которой от общего суждения переходят к частному суждению. Дедукция представляет собой форму умозаключения, состоящую в том, что новое суждение выводится чисто логическим путём, то есть по определённым правилам логического вывода (следования) из некоторых известных суждений.
Впервые теория дедукции (логического вывода) была разработана Аристотелем. Особое развитие она получила в виде теории доказательств в математической логике.
Существенным различием между индукцией и дедукцией является характер заключения. Заключение по индукции лишь правдоподобно, заключение по дедукции достоверно, если истинны посылки и верно применено одно из правил логического вывода.
Приведём пример дедуктивного умозаключения.
Суждения: любой квадрат – ромб, любой ромб – параллелограмм. Дедуктивный вывод: любой квадрат – параллелограмм. Правило вывода – правило силлогизма. Суждение «любой квадрат – параллелограмм» истинно, так как истинны посылки и в основе его вывода использовано правило силлогизма. Широкое применение дедукции в математике обусловлено аксиоматическим методом построения математических теорий, основанном на некоторых предложениях, истинность которых признаётся без доказательств. Истинность же остальных предложений этой теории устанавливается с помощью дедуктивных доказательств, то есть все остальные предложения теории логически выводятся (дедуцируются) из предшествующих им предложений. Вот почему математику называют дедуктивной наукой.
Литература
1. Методика и технология обучения математике. Курс лекций: пособие для вузов / под науч. ред. Н.Л. Стефановой. – М., Дрофа, 2005.
2.Саранцев Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / Г. И. Саранцев. - М.: Просвещение, 2002.
3. Методика преподавания математики в средней школе: общая методика, Учеб. пособие для студентов пед. ин-тов / составители Р. С. Черкасов, А. А. Столяр. – М., Просвещение, 1985.
4. Груденов Я. И. Совершенствование методики работы учителя математики: кн.для учителя / Я.И. Груденов. – М. Просвещение, 1990.
Вопросы и задания к зачёту по общей методике обучения математике
Дата добавления: 2020-07-18; просмотров: 1328;













