Доказательство правильности

Пусть l(v) — длина кратчайшего пути из вершины a в вершину v. Докажем по индукции, что в момент посещения любой вершины z, d(z)=l(z).
База. Первой посещается вершина a. В этот момент d(a)=l(a)=0.
Шаг. Пускай мы выбрали для посещения вершину 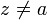. Докажем, что в этот момент d(z)=l(z). Для начала отметим, что для любой вершины v, всегда выполняется 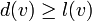(алгоритм не может найти путь короче, чем кратчайший из всех существующих). Пусть P — кратчайший путь из a в z, y — первая непосещённая вершина на P, x — предшествующая ей (следовательно, посещённая). Поскольку путь P кратчайший, его часть, ведущая из a через x в y, тоже кратчайшая, следовательно l(y)=l(x)+w(xy). По предположению индукции, в момент посещения вершины x выполнялось d(x)=l(x), следовательно, вершина y тогда получила метку не больше чем d(x)+w(xy)=l(x)+w(xy)=l(y). Следовательно, d(y)=l(y). С другой стороны, поскольку сейчас мы выбрали вершину z, её метка минимальна среди непосещённых, то есть 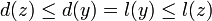. Комбинируя это с 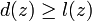, имеем d(z)=l(z), что и требовалось доказать.

Поскольку алгоритм заканчивает работу, когда все вершины посещены, в этот момент d=l для всех вершин.