Энергетические показатели асинхронных электроприводов
Для оценки энергетических показателей асинхронных электроприводов следует определить не только его КПД, но и коэффициент мощности.
Для оценки КПД воспользуемся схемой замещения асинхронного двигателя (рис. 5.5). Активная мощность, потребляемая из сети, равна
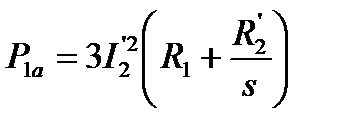 . (5.36)
. (5.36)
С другой стороны, из (5.17) и рис. 5.6
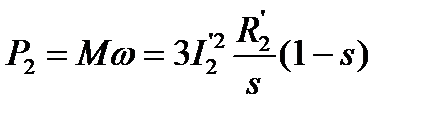 . (5.37)
. (5.37)
Тогда
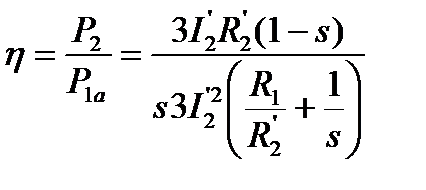 ;
;
Окончательно
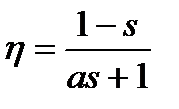 . (5.38)
. (5.38)
Для крупных машин, у которых 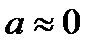
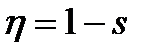 . (5.39)
. (5.39)
Следует отметить, что значения КПД, рассчитанные по формулам (2.38), (2.39), не учитывают потери в стали статора и ротора, механические потери, и потери, обусловленные высшими гармоническими составляющими. Они относятся к постоянным потерям и относительно невелики. Поэтому, как и для электроприводов постоянного тока, приведённые формулы позволяют оценить значение КПД двигателя в целом.
При работе двигателя в номинальном режиме
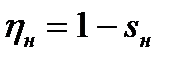 .
.
Тогда для современных асинхронных двигателей с короткозамкнутым ротором с 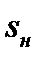 =0,01
=0,01 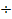 0,05 (меньшие значения для двигателей большей мощности – сотни киловатт)
0,05 (меньшие значения для двигателей большей мощности – сотни киловатт)
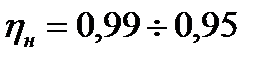 ,
,
перегрузочная способность 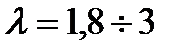 , кратность пускового тока
, кратность пускового тока 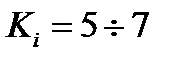 , кратность пускового момента
, кратность пускового момента 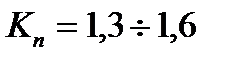 .
.
Коэффициент мощности для главной цепи двигателя без учёта намагничивающего контура может быть определён (схема замещения рис. 5.5) по формуле
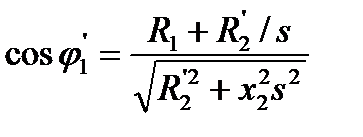 .
.
Учитывая (5.20), это выражение можно переписать в следующем виде
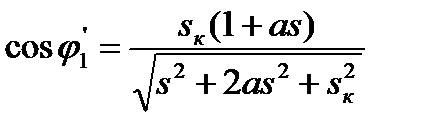 . (5.40)
. (5.40)
Из последнего уравнения видно, что коэффициент мощности рассматриваемой цепи двигателя уменьшается с увеличением скольжения. На рис. 5.8,а приведена зависимость 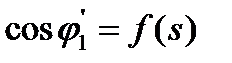 . Для крупных машин
. Для крупных машин 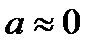 и при
и при 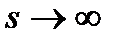
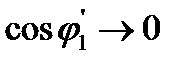 .
.
Величина 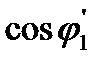 не характеризует потребление реактивной мощности двигателем. Для анализа вопроса необходимо определить величину
не характеризует потребление реактивной мощности двигателем. Для анализа вопроса необходимо определить величину 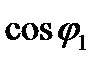
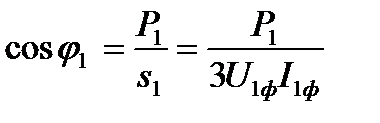 .
.
Из упрощенной круговой диаграммы можно определить
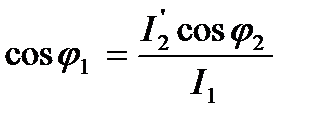 . (5.41)
. (5.41)
Модуль вектора тока статора может быть определён из следующего соотношения ( см. рис. 5.8)
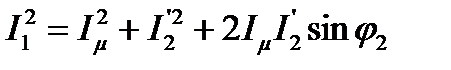 . (5.42)
. (5.42)
В соответствии со схемой замещения (рис. 5.5)
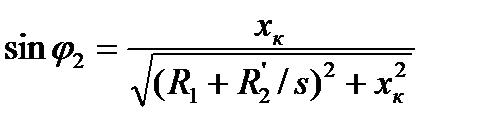 .
.
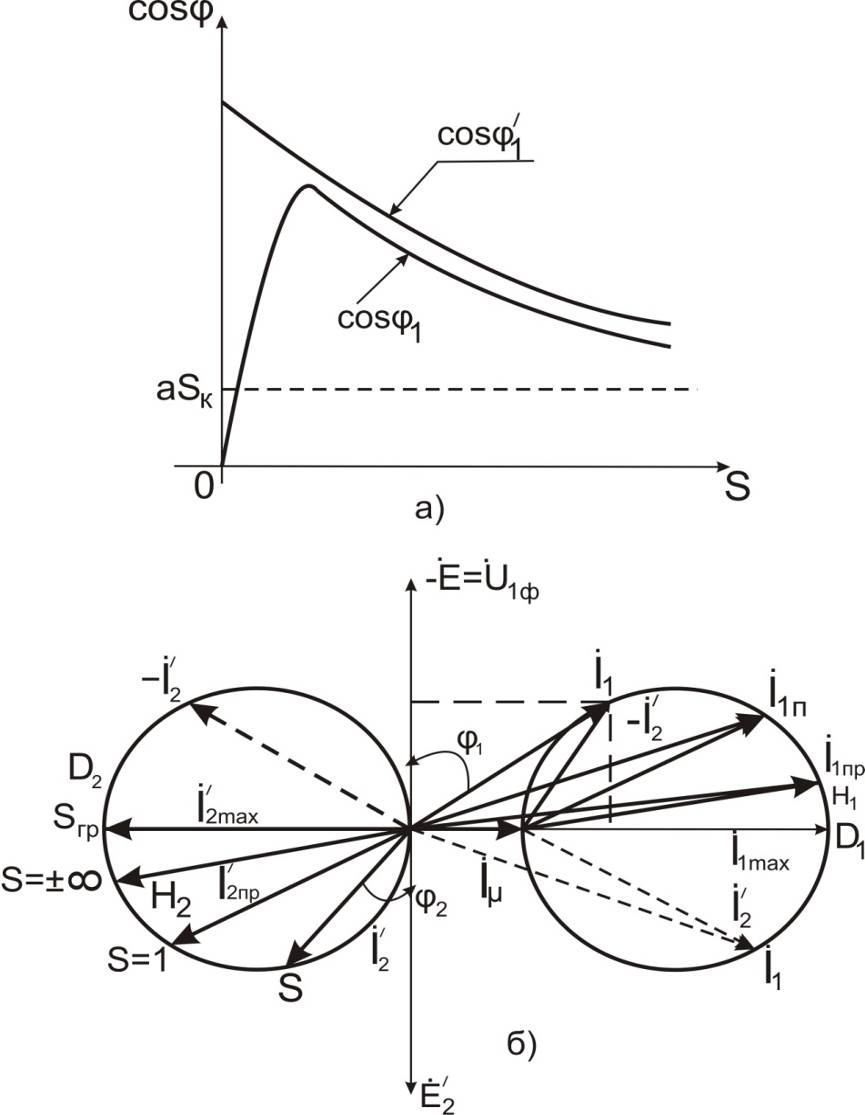
Рис. 5.8. Зависимости 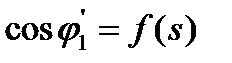 (а) и упрощенная круговая диаграмма асинхронного двигателя (б)
(а) и упрощенная круговая диаграмма асинхронного двигателя (б)
Заменяя в последнем выражении в соответствии с (5.20) 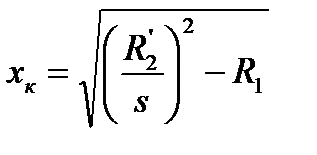 и учитывая, что
и учитывая, что 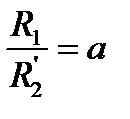 , после преобразований находим
, после преобразований находим
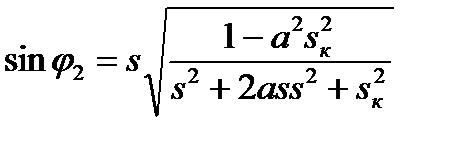 . (5.43)
. (5.43)
Подстановка в (5.42) этого значения 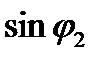 , а также
, а также 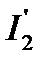 по формуле
по формуле
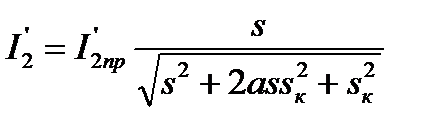 (5.44)
(5.44)
в (5.42) позволяет получить
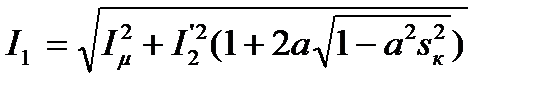 , (5.45)
, (5.45)
где 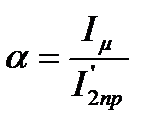 .
.
В большинстве случаев 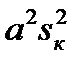 <<1и
<<1и
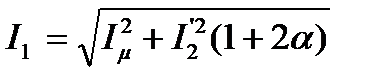 . (5.46)
. (5.46)
Входящий в (5.46) коэффициент 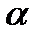 может быть принят для выпускаемых промышленностью двигателей в пределах 0,13
может быть принят для выпускаемых промышленностью двигателей в пределах 0,13 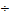 0,115. Зависимость
0,115. Зависимость 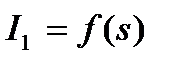 представлена на рис. 5.7,б.
представлена на рис. 5.7,б.
Для крупных машин, у которых 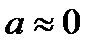 , после подстановки в (5.41) величины
, после подстановки в (5.41) величины 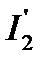 (5.44) и
(5.44) и 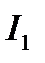 (5.46) получим формулу
(5.46) получим формулу
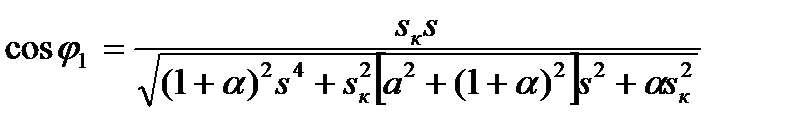 , (5.47)
, (5.47)
по которой и построена зависимость 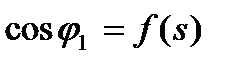 (рис. 5.8,а).
(рис. 5.8,а).
Из анализа (5.47) следует, что 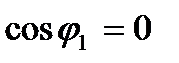 при
при 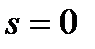 , т.е. в режиме идеального холостого хода двигатель потребляет из сети чисто реактивный ток намагничивания. Это же следует и из круговой диаграммы (рис. 5.8,б). При увеличении
, т.е. в режиме идеального холостого хода двигатель потребляет из сети чисто реактивный ток намагничивания. Это же следует и из круговой диаграммы (рис. 5.8,б). При увеличении 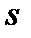
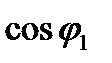 нарастает до значения
нарастает до значения
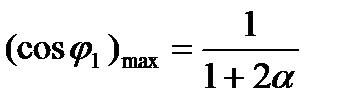 (5.48)
(5.48)
при скольжении
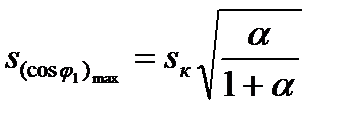 ,
,
а при дальнейшем увеличении скольжения 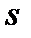
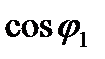 уменьшается.
уменьшается.
В номинальном режиме работа двигателя характеризуется почти наибольшим значением 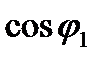 , т.к.
, т.к. 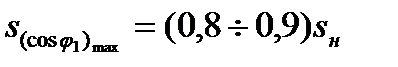 .
.
Таким образом, 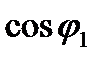 для асинхронных двигателей лежит в пределах
для асинхронных двигателей лежит в пределах
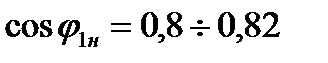 .
.
Дата добавления: 2019-02-08; просмотров: 1062;











