Статические электромеханические и механические характеристики асинхронного электропривода

Для качественной оценки электромеханических свойств асинхронного электропривода и количественных расчётов необходимо упростить схему замещения фазы АД (рис. 5.4) путём вынесения контура намагничивания на зажимы статора, тем самым пренебрегая влиянием параметров обмотки статора 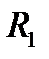, 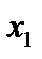на магнитный поток (рис. 5.5).

Принятая Г-образная схема замещения асинхронного двигателя справедлива при следующих допущениях:

а) параметры всех цепей двигателя постоянны, т.е. 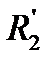не зависит от частоты и явления вытеснения тока в роторе, а насыщение магнитной системы не влияет на реактивные сопротивления 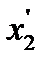и ;

б) полная проводимость намагничивающего контура (сопротивление 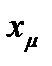и 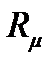) неизменна, а намагничивающий ток не зависит от нагрузки (тока 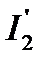) и всегда пропорционален приложенному напряжению;

в) не учитываются добавочные потери и паразитные моменты, создаваемые высшими гармониками МДС и токов двигателя.

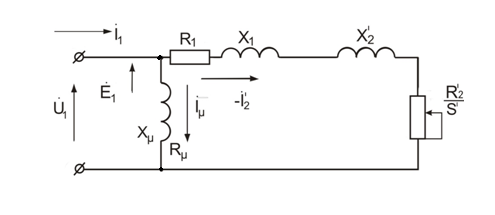
Рис. 5.5. Упрощённая схема замещения асинхронной машины

Уравнение механической характеристики 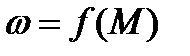получим, приравняв потери в роторной цепи, выраженные через механические и электрические величины.

Энергетическая диаграмма асинхронной машины в двигательном режиме представлена рис.5.6

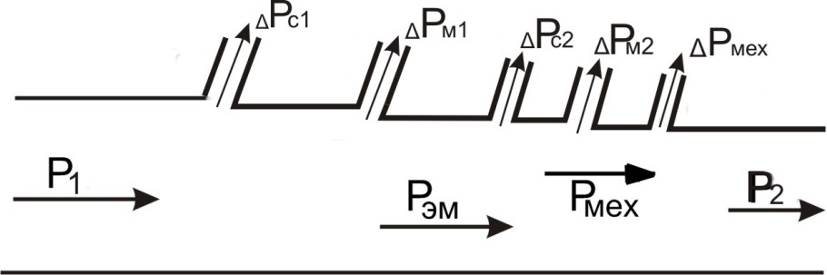
Рис. 5.6. Энергетическая диаграмма асинхронной машины в двигательном режиме

Мощность, потребляемая двигателем из сети, если пренебречь потерями в стали статора 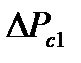и потерями в меди статора 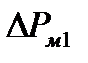, примерно равна электромагнитной мощности

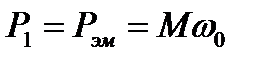, (5.13)

где M - электромагнитный момент, а мощность на валу при пренебрежении потерями 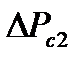, 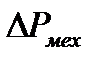определится как

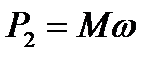. (5.14)

Тогда потери в роторной цепи

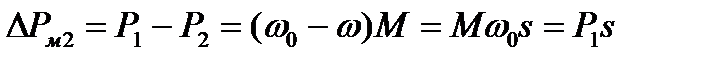. (5.15)

С другой стороны при выражении этих потерь через электрические величины, получим

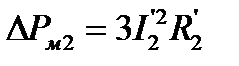, (5.16)

откуда

. (5.17)

Из (5.17) следует, что для определения зависимости 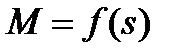асинхронного двигателя необходимо знать зависимость .

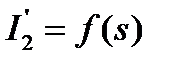В соответствии со схемой замещения (рис. 5.5) ток ротора найдётся по формуле

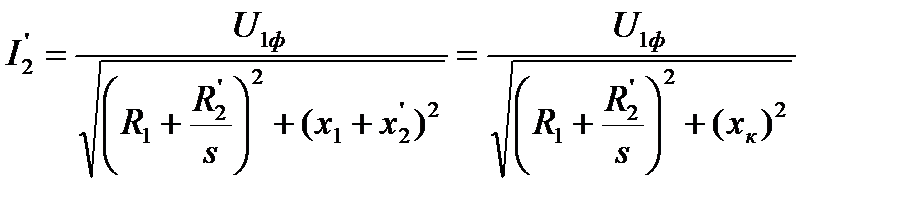(5.18)

где 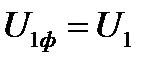- фазное значение напряжения обмотки статора;

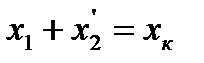- индуктивное фазное сопротивление короткого замыкания.

Подстановка (5.18) в (5.17) даёт уравнение механической характеристики

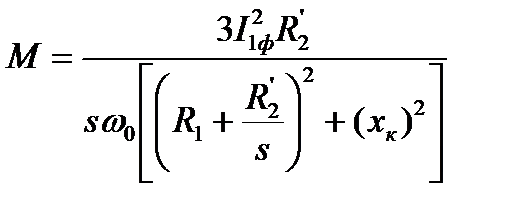. (5.19)

Анализ этого уравнения показывает, что зависимость 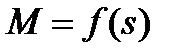имеет максимум, так как при скольжении 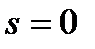, 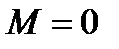. Максимальное значение момента 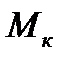называется критическим. Соответствующее ему скольжение ( ) также называется критическим. Согласно общему правилу нахождения экстремума функции, необходимо определить производную 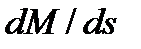уравнения (5.19), приравнять её к нулю и определить критическое скольжение

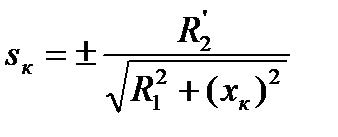. (5.20)

Подставляя в (5.19), находим

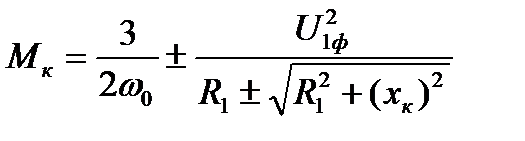. (5.21)

Знаки ( 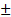) в (5.20) означают, что максимум момента может иметь место при 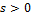в двигательном режиме и при в генераторном режиме. Знак плюс в (5.21) соответствует 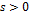, а минус 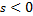. Из (5.21) также видно, что при работе в генераторном режиме с рекуперацией энергии критический момент больше, чем в двигательном режиме.

Из (5.19) и (5.21) с учётом (5.20) может быть получена другая формула для механической характеристики

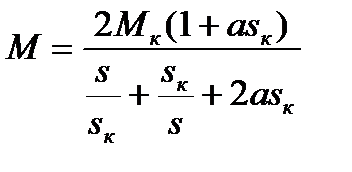, (5.22)

в которой параметрами являются величины , , 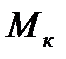и 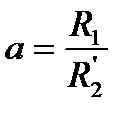. На практике иногда полагают, что 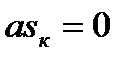. Это обычно не приводит к существенным погрешностям при 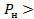5кВт. В этом случае можно воспользоваться упрощёнными формулами

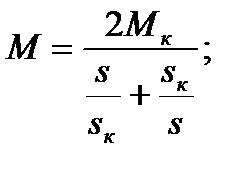(5.23)

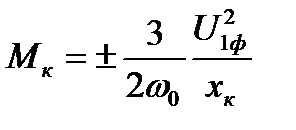; (5.24)

. (5.25)

Основное преимущество записи механической характеристики в виде (5.23) по сравнению с (5.22) заключается в том, что для (5.23) достаточно знать лишь параметры, которые обычно указываются в каталогах. В каталогах на асинхронные двигатели, помимо номинальных данных 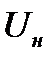, , 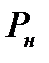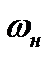и др., приводится значение 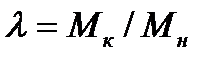, которое называют также перегрузочной способностью.

Другие параметры и величины можно определить по следующим формулам:

номинальный момент

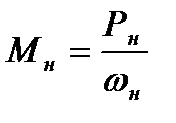, (5.26)

номинальное скольжение

, (5.27)

критическое значение скольжения для машин малой мощности с .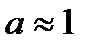

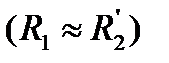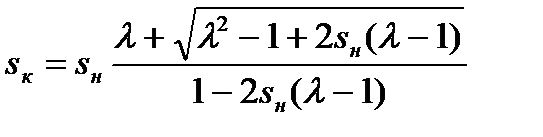, (5.28)

для крупных двигателей ( 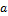=0)

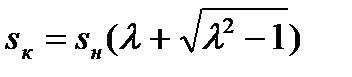. (5.29)

Для анализа формы механической характеристики и режимов работы асинхронного электропривода воспользуемся формулами (5.23) – (5.29). На рис. 5.7 представлена механическая характеристика асинхронного двигателя .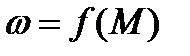

Как и для двигателей постоянного тока, у асинхронного двигателя имеется естественная механическая и электромеханическая характеристики при 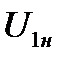, , 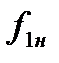и отсутствии добавочных сопротивлений в статорной и роторной цепях. Все другие характеристики искусственные.

Проанализируем форму механической и скоростной характеристик, представленной на рис. 5.7.

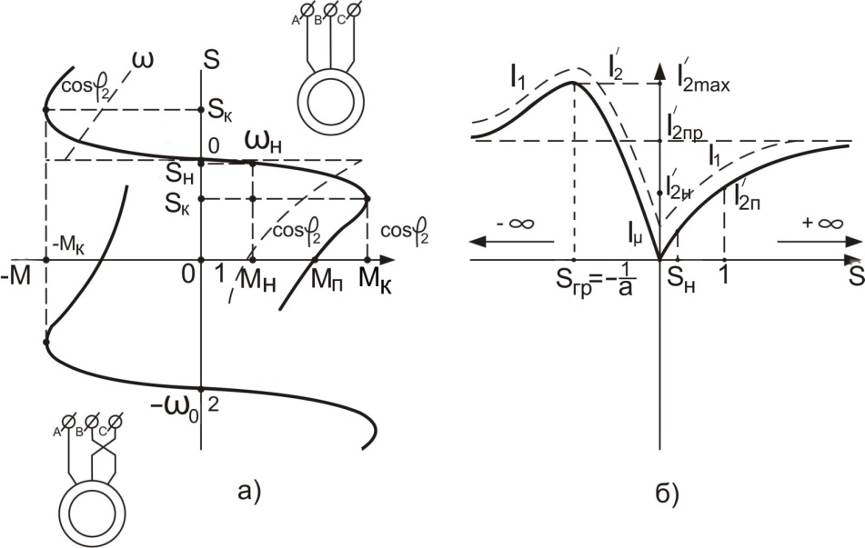Рис. 5.7. Зависимости 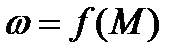, 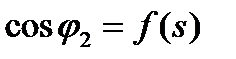(а), и 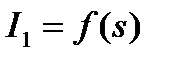, (б) асинхронного двигателя

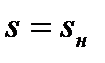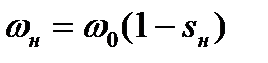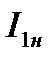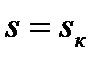При изменении скольжения от 0 до 1 асинхронная машина работает в двигательном режиме. Скольжению S=0 соответствует идеальный холостой ход, ротор двигателя имеет синхронную скорость . Скольжение свидетельствует о номинальной скорости вращения ротора , двигатель при этом развивает номинальный момент и по обмоткам протекают номинальные токи , . При скольжении двигатель развивает максимальный (критический) момент 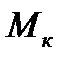. Скольжению 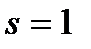соответствует пусковой момент

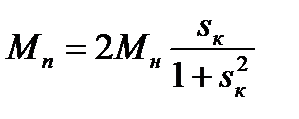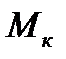< , (5.30)

который при 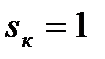равен .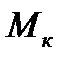

При скольжении 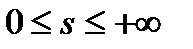асинхронная машина работает в режиме противовключения.

Скольжению 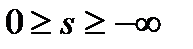соответствует генераторный режим параллельно сетью (рекуперативное торможение), в котором > .

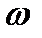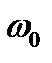Зависимость 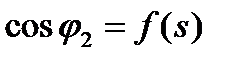можно получить из схемы замещения рис. 5.4

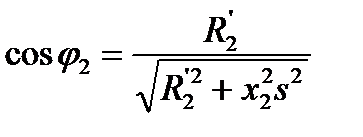, (5.31)

следовательно, 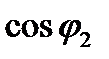при возрастании модуля скольжения монотонно убывает, стремясь при 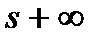к нулю (рис. 5.7,а).

Как следует из формулы (5.10) с изменением скольжения от нуля до 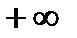ток ротора монотонно увеличивается до (рис. 5.7,б)

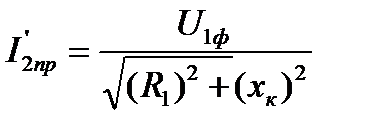. (5.32)

При 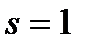пусковой ток определяется по формуле

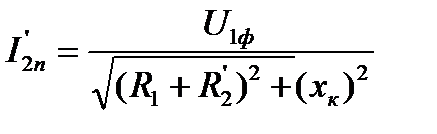(5.33)

и составляет на естественной характеристике 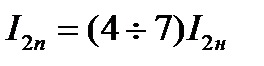. Для уменьшения пусковых токов, необходимо включать в роторную цепь (АД с фазным ротором) активные или индуктивные сопротивления, а также в статорную цепь двигателей.

В генераторном режиме параллельно с сетью при изменении 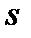ток растёт до своего максимального значения при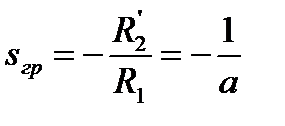

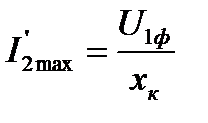, (5.34)

а затем монотонно снижается до 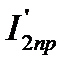(рис. 5.7,б). При 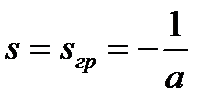вектор тока ротора перпендикулярен вектору 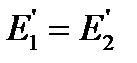и является чисто реактивным, и рекуперация энергии в сеть прекращается.

Если принять магнитный поток Ф=const, то, как следует из формулы (5.4) момент двигателя достигает максимального значения 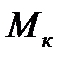при

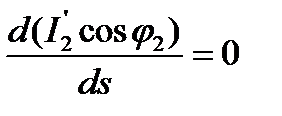, (5.35)

где ;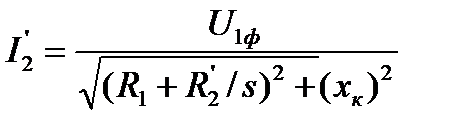

.

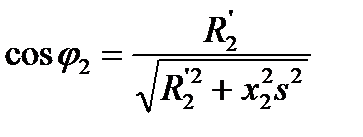Максимальное значение момента двигателя в двигательном режиме определяет его перегрузочную способность. При этом нужно иметь в виду, что 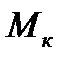пропорционален квадрату приложенного напряжения 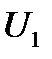, вследствие чего асинхронный двигатель весьма чувствителен к колебаниям напряжения сети. В каталожных данных для асинхронных двигателей указывается перегрузочная способность двигателя при номинальном напряжении 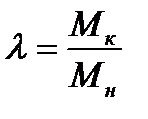. При определении момента допустимой перегрузки следует учитывать возможное снижение напряжения сети на 10%

.

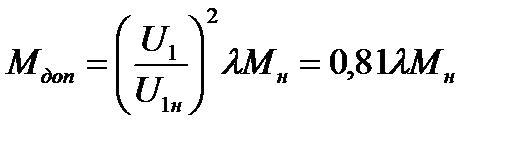В таблице 5.1 для некоторых серийно выпускаемых двигателей приводятся значения перегрузочной способности и кратности пускового момента по отношению к номинальному .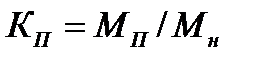

Таблица 5.1.

Коэффициенты 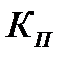и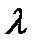

	Серия или модификация исполнения двигателя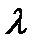
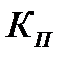
	Двигатели с к/з ротором единой серии 4А: с повышенным скольжением с ротором нормального исполнения с повышенным пусковым моментом	1,8-2,4 1,7-2,2   2,2	1,7-2,2 1-1,9   1,7-1,8
	Двигатели с к з. ротором краново – металлургической серии 4МТК	2,6 – 3,6	2,5-3,3
	Двигатели с фазным ротором модификация 4А	1,7-2,0	-
	Двигатели с фазным ротором краново – металлургической серии 4МТ	2,3-3,0	-