Перемещения и деформации

В сопромате расчеты конструкций производят с использованием расчетных схем. На расчетной схеме вместо бруса изображают его ось. Нагрузку, приложенную к небольшим участкам поверхности бруса, заменяют сосредоточенными силами. Нагрузку, приложенную к участкам больших размеров, составляющих существенную часть его длины, изображают распределенной силой (рис. 2.1).

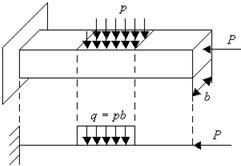
Рис. 2.1

Перемещения возникают за счет деформации тела. В теории предполагается, что у нас действуют только упругие деформации. Известны два вида деформаций: изменение длины и сдвиг (рис. 2.2).

В первом случае происходит уменьшение или увеличение длины отрезка. Во втором искажение первоначально прямого угла.

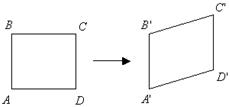
Рис. 2.2

Элемент ABCD расположен в поперечном сечении бруса. Точка А, начало отсчета, считается неподвижной. Внутренние силы в сечении можно разложить на две составляющие: касательную (включает силы расположенные в плоскости сечения) и нормальную (перпендикулярна плоскости сечения).

Метод сечений

Рассмотрим элемент конструкции, на который действует система внешних сил, находящихся в равновесии (рис. 2.3). Причем в число внешних сил входят как заданные активные силы, так и реакции связи.

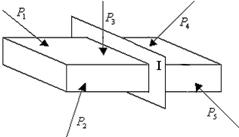
Рис. 2.3

Мысленно рассечем элемент плоскостью I. Силы воздействия отсеченной левой части на правую для всего элемента считаются внутренними.

На основании известного закона механики (действие равно противодействию), эти силы равны по величине и противоположны по направлению. Каждому из усилий соответствует определенный вид деформации бруса: продольной силе N – растяжение-сжатие, моменту 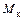– кручение, моментам 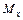и – и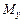згиб (рис. 2.4).

Mк

Mк

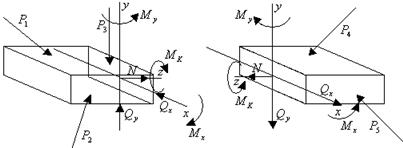
Рис. 2.4

Все эти усилия являются внутренними. Прием определения этих усилий называется методом сечений. Так как внешние силы уравновешиваются внутренними, то проекция на какую-либо ось внутреннего усилия, действующего со стороны левой части на правую, равна проекции на эту ось всех внешних сил, приложенных к левой части.

Момент относительно какой-либо оси внутренних усилий в сечении, действующий со стороны левой части на правую, равен моменту всех внешних сил, действующих со стороны левой части, относительно этой оси.

2.5. Напряжения

Внутренние силы в сечении можно разложить на две составляющие: нормальную и касательную. Первая составляющая перпендикулярна плоскости сечения, а вторая расположена в этой плоскости.

Напряжение – интенсивность касательных сил в рассматриваемой точке сечения называется касательным напряжением:

,

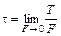где T – касательная сила; F – площадь сечения.

Интенсивность нормальных сил называется нормальным напряжением:

.

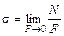Нормальные и касательные напряжения являются составляющими полного напряжения (эквивалентного):

.

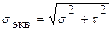Величины напряжений s и t в каждой точке элемента зависят от направления сечения, проведенного через эту точку, т.е. если сечение расположено по отношению к горизонтальной оси под углом не равным 90°, то величины s и t изменятся.

Вопросы для самопроверки

К разделу 2

1. В чем заключаются задачи курса «Сопротивление материалов»?

2. Какие гипотезы используются при изучении курса «Сопротивление материалов»?

3. Что называют прочностью, жесткостью, устойчивостью детали?

3. Какие силы в сопротивлении материалов считают внешними? Какие силы являются внутренними?

4. Какими методами определяют внешние силы? Как называют метод для определения внутренних сил?

5. Как классифицируются нагрузки, действующие на части машин и сооружений?

6. Что такое сосредоточенная сила, распределенная нагрузка и момент? 7. Поясните суть метода сечений.

7. Дайте определение понятия «напряжения» и какие виды напряжения вы знаете?

8. В каких единицах измеряются напряжения?

9. Чем отличаются нормальные напряжения от касательных?

10. Что оценивается величиной напряжений?