Определение деформаций при растяжении-сжатии

Нормальным напряжениям соответствует деформация растяжения-сжатия, а касательным – сдвиг.

Прямой брус длиной l и нагруженный силой P удлиняется на величину Dl (рис. 3.5):

,

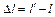где 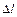– абсолютная деформация бруса (полная деформация).

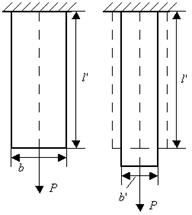
Рис. 3.5

Линейную деформацию 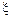называют относительным продольным удлинением:

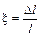. (3.6)

Происходит также изменение поперечных размеров бруса. Относительная поперечная деформация может быть рассчитана по формуле

.

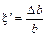Экспериментально установлено, что при напряжениях, не превышающих предела упругости, выполняется уравнение:

;

,

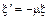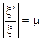где 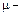коэффициент поперечной деформации (коэффициент Пуассона), который определяется экспериментально и изменяется в пределах от 0 – для пробки, до 0,5 – для резины; для стали .

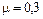Установлено, что когда напряжение в брусе не превышает предела пропорциональности, выполняется условие

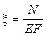, (3.7)

где Е – коэффициент, зависящий от физических свойств материала (модуль упругости).

Параметр Е, наряду с m, характеризует упругие свойства материала.
В системе СИ измеряется в паскалях [Па].

Для стали 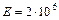кг/см²; для меди 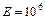кг/см²; для условного дерева 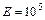кг/см².

Произведение EF называется жесткостью поперечного сечения бруса а, учитывая что 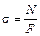, уравнение (3.7) примет вид

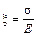, (3.8)

или

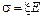. (3.9)

Абсолютное удлинение бруса выражается зависимостью, полученной из (3.6) и (3.7):

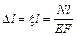. (3.10)

Формулы (3.8) – (3.10) являются математическим выражением закона Гука, который звучит так: абсолютная продольная деформация прямо пропорциональна продольной силе (при постоянной жесткости сечения EF); или относительная продольная деформация прямо пропорциональна нормальному напряжению.