Растяжение и сжатие стержня и стержневых сиСтем

Растяжение-сжатие прямого бруса

Различают простое и внецентренное растяжение-сжатие (рис. 3.1). При простом, линия действия силы совпадает с осью бруса. Если не совпадает, а параллельна ей, то это – внецентренное растяжение-сжатие.

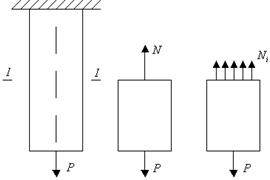
Рис. 3.1

Из уравнения проекций на вертикальную ось имеем:

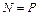, (3.1)

где Р – внешняя сила; N – внутреннее усилие.

Метод сечений:для нахождения внутренних усилий тело мысленно разрезают на две части и рассматривают равновесие той части, которая не соприкасается с заделкой.

При растяжении-сжатии гипотеза плоских сечений дополняется еще одним пунктом: в поперечных сечениях достаточно далеко удаленных от точки приложения сил нормальные силы распределяются по сечению равномерно, а касательные отсутствуют.

Нормальное напряжение характеризует величину внутренних усилий приходящихся на единицу площади сечения:

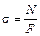. (3.2)

Правило знаков: нормальные усилия и напряжения положительны при растяжении и отрицательны при сжатии.

Условие прочности при растяжении и сжатии

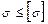, (3.3)

где 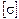– допускаемое нормальное напряжение (справочная величина, физико-механическая характеристика материала). Это наибольшее напряжение, при котором материал конструкции может надежно и долго работать.

Решая совместно уравнения (3.2) и (3.3), имеем

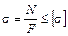. (3.4)

Это уравнение прочности при растяжении-сжатии. С его помощью возможно решение трех типов задач, но наиболее часто решается задача подбора площади сечения F при известных значениях N и 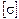. Тогда

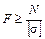. (3.5)

Например, для круга

; .

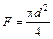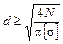Для прямоугольного сечения должно быть задано соотношение сторон:

; ; ,

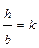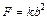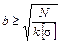где h – высота; b – основание.

Значение продольной силы в каждом частном случае можно легко определить с помощью метода сечений. Для нахождения напряжения 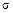в каждой точке поперечного сечения, необходимо знать закон распределения по сечению, который обычно изображается графиком, показывающим их изменение по высоте балки (эпюра нормальных напряжений).