В случае переменной массы
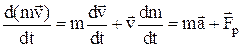 ,
,
где 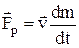 – реактивная сила.
– реактивная сила.
При движении по кривой результирующая сила может быть разложена на две составляющие (рис. П 1.13):
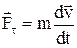 ;
; 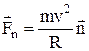 ,
,
где R – радиус кривизны траектории;
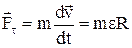 – тангенциальная составляющая (касательная сила);
– тангенциальная составляющая (касательная сила);

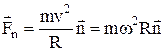 – нормальная составляющая (центростремительная сила).
– нормальная составляющая (центростремительная сила).
Основной закон классической динамики – инвариантен при переходе от одной инерциальной системы к другой, при этом
ma= F; ma' = F'; F= F'.
Третий закон классической динамики –силы, с которыми взаимодействуют два тела, равны по величине и противоположны по направлению. Силы действия и противодействия приложены к разным телам и никогда не уравновешивают друг друга (рис. П1.14):
F12 = -F21.
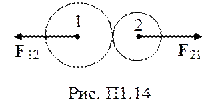
Импульс силы –мера действия силы за некоторый промежуток времени:
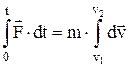 .
.
Силы инерции обусловлены ускоренным движением системы отсчета по отношению к неподвижной системе. Различают:
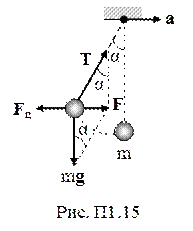
1) силы, действующие на тело при ускоренном поступательном движении системы отсчета (рис. П1.15):
ma’=ma + Fин,
где a’ – ускорение тела в неинерциальной системе отсчета;
a – ускорение тела в инерциальной системе отсчета;
Fин – сила инерции.
2) силы, действующие на тело, покоящееся во вращающейся системе отсчета (рис. П 1.16):
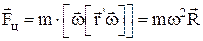 ,
,
где Fц – центробежная сила инерции;
w – угловая скорость вращающейся системы отсчета;
r’ – радиус-вектор тела относительно начала вращающейся системы отсчета;
R – перпендикулярная к оси вращения составляющая r’.
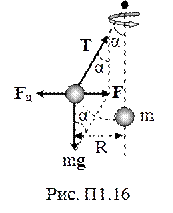
3) силы, действующие на тело, движущееся во вращающейся системе отсчета (рис. П1.17):
Fк =2m×[v’ ω],
где Fк – сила Кориолиса;
v’ – скорость движения тела;
w – угловая скорость вращающейся системы отсчета.
Основной закон динамики для неинерциальных систем отсчета:
ma’= F + Fин + Fц+ Fк,
где F, Fин, Fц, Fк – ранее рассмотренные силы, действующие в неинерциальных системах отсчета.
Основная задача динамики вращательного движения – нахождение угловых ускорений, сообщаемых известными силами.
Момент инерции – скалярная физическая величина, характеризующая инертность тела при вращательном движении.
Момент инерции материальной точки относительно неподвижной оси вращения – физическая величина, равная произведению массы материальной точки на квадрат расстояния до оси или центра вращения (рис. П1.18):
DI = Dm×r2.

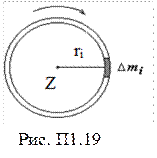
Момент инерции тела относительно оси z – физическая величина, равная сумме моментов инерции отдельных материальных точек тела относительно той же оси вращения (рис. П1.19):
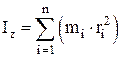 ;
;  ,
,
где mi – масса i-й точки;
ri – расстояние i-й точки до оси z;
ρ – плотность вещества, из которого состоит тело;
V – объем тела.
Теорема Штейнера – момент инерции тела относительно произвольной оси z равен сумме момента инерции того же тела I0 относительно оси, параллельной данной и проходящей через центр масс, и произведения массы тела m на квадрат расстояния между осями (а):
Iz = I0 + mа2.

На рисунке П1.20 представлено применение теоремы Штейнера к расчету момента инерции диска относительно оси ОО', параллельной оси О1О1'.
Главные оси инерции – три взаимно перпендикулярных свободных оси вращения тела произвольной формы, проходящие через его центр масс.
Момент импульса материальной точки относительно неподвижной оси вращения (L) – векторная физическая величина, модуль которой равен произведению модуля импульса на плечо (рис. П1.21):
çLê= êpê×l.
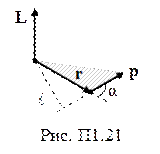
В векторной форме
L=[r´p] = [r´mv],
где m – масса материальной точки;
v – скорость материальной точки;
l – плечо (кратчайшее расстояние от направления импульса до оси вращения).
Момент импульса системы относительно неподвижной оси вращения z –проекция на эту ось вектораL (момента импульса системы):
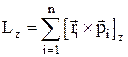 ,
,
где ri, pi – радиус-вектор и импульс i-й материальной точки;
n – общее число точек в системе.
Связь момента импульса тела с вектором угловой скорости ω и моментом инерции
L= Iω.
Момент силы относительно центра вращения или неподвижной оси вращения – векторная физическая величина, модуль которой равен произведению модуля силы на плечо (рис. П1.22):
çMç=çFçl,
где l – плечо силы – кратчайшее расстояние от линии действия силы до центра вращения.

В векторной форме
M=[r´F].
Главный или результирующий момент сил относительно неподвижной оси вращенияравен векторной сумме моментов слагаемых сил:
 .
.
Моменты сил относительно осей, которые перпендикулярны и параллельны оси вращения, равны нулю.
Основной закон динамики вращательного движения твердых (недеформирующихся) тел, для которых I=const (второй закон динамики для вращательного движения):
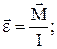 M= I∙ε;
M= I∙ε;  .
.
Импульс вращающего момента – произведение вращающего момента на время его действия:
M×dt = dL.
Осциллятор– физическая система, совершающая колебания; система, у которой величины, описывающие ее, периодически меняются с течением времени.
Гармонический осциллятор– механическая система, совершающая колебания около положения устойчивого равновесия, описывающие величины которой изменяются по гармоническому закону (закону синуса или косинуса).
Уравнение движения гармонического осциллятора:
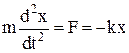 ;
; 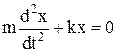 ;
;  ,
,
где a = d2x/dt2 = –ω02x – ускорение материальной точки;
F – возвращающая сила, которая стремится вернуть систему в положение равновесия (F = –mω02x = –kx);
x – смещение;
k = mω02 – коэффициент возвращающей силы. Он численно равен возвращающей силе, вызывающей единичное смещение.
Решение уравнения движения гармонического осциллятора:
x = x0×sin (ω0t + φ0).
Уравнение гармонических колебаний в комплексном виде:
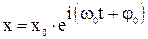 .
.
В теории колебаний принимается, что величина x равна вещественной части комплексного выражения, стоящего в этом выражении справа.
Дифференциальное уравнение гармонического колебательного движения:
 .
.
Решением дифференциального уравнения гармонических колебанийявляется выражение вида
x = x0 sin (w0t + j0),
где k = m w02 – коэффициент возвращающей силы;
x – смещение материальной точки;
x0 – амплитуда колебаний;
w0 = 2p/Т = 2pn – круговая (циклическая частота);
n = 1/T – частота колебаний;
T – период колебаний;
j = (w0t + j0) – фаза колебаний;
j0 – начальная фаза колебаний.
Примеры гармонических осцилляторов:
а) пружинный маятник – тело массой m (рис. П1.23), подвешенное на пружине, совершающее гармоническое колебание.
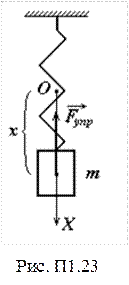
Упругие колебания совершаются под действием упругих сил:
F= –k∙Dl,
где k = m wo2 – коэффициент жесткости;
Dl – относительное удлинение.
Уравнение движения пружинного маятника:
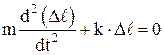 ;
; 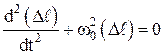 ,
,
где 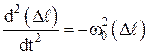 ;
;
Dl – величина деформации.
Решение уравнения движения пружинного маятника:
Dl = (Dl)0×sin (ω0t + φ0).
Круговая частота, частота и период колебаний пружинного маятника:
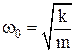 ;
; 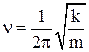 ;
; 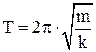 ;
;
б) физический маятник – твердое тело, совершающее гармоническое колебательное движение относительно оси, не совпадающей с центром масс (рис. П1.24).
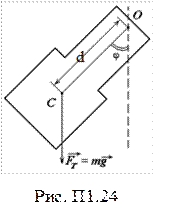
Уравнение движения физического маятника:
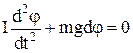 .
.
Решение уравнения движения физического маятника:
j = j0×sin (ω0t + α),
где α – начальная фаза колебаний.
Круговая частота, частота и период колебаний физического маятника:
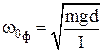 ;
; 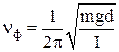 ;
;  ;
;  ,
,
где L = I/md – приведенная длина физического маятника – длина такого математического маятник, период колебаний которого равен периоду колебаний физического маятника;
I – момент инерции физического маятникa относительно оси колебаний;
m – масса физического маятника;
d – расстояние между осью колебаний и центром масс;
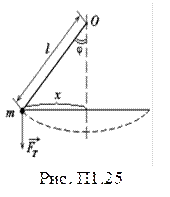
в) математический маятник – тело массой m, размерами которого можно пренебречь, подвешенное на невесомой, нерастяжимой нити (рис. П1.25).
Круговая частота, частота и период колебаний математического маятника:
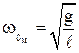 ;
; 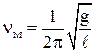 ;
; 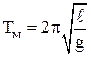 .
.
Приведенная длина физического маятника – величина, численно равная длине такого математического маятника, период колебаний которого равен периоду колебаний физического маятника:
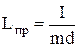 .
.
Крутильные колебания – колебания, совершающиеся под действием закручивающего момента, пропорционального углу закручивания (колебания диска, подвешенного на стальной нити):
M= – Da,
где 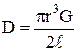 – коэффициент крутильной жесткости;
– коэффициент крутильной жесткости;
G – модуль сдвига;
r – радиус нити;
l – длина нити.
Дата добавления: 2022-02-05; просмотров: 539;











