Уравнение движения электропривода
В простейшем случае имеет вид:
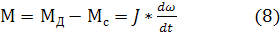 ,
,
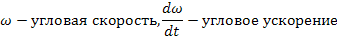
т.к. на практике могут быть разные соотношение между
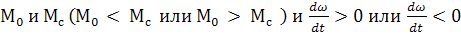
Обобщенная формула уравнения (8)
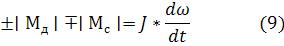
Уравнение иногда называют уравнением механического равновесия электропривода. Если умножить все члены этого уравнения на угловую скорость ω, то вместо уравнения равенства моментов получим уравнение равенства мощностей
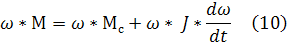
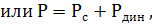
где Р- мощность, подводимая к нагрузки от двигателя, 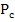 - мощность, требуемая для преодоления сопротивления трения или просто сопротивление нагрузки,
- мощность, требуемая для преодоления сопротивления трения или просто сопротивление нагрузки,  - динамическая мощность, идущая на ускорение или замедление системы.
- динамическая мощность, идущая на ускорение или замедление системы.
Правая часть в выражениях (8) и (9) представляет собой динамический момент
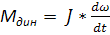 , возникающий в случае если сумма моментов отлична от нуля,
, возникающий в случае если сумма моментов отлична от нуля,
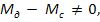 если
если 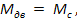 то режим работы привода при этом условии называют установившемся или статическим.
то режим работы привода при этом условии называют установившемся или статическим.
Если же 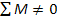 , то режим называют переходным или динамическим.
, то режим называют переходным или динамическим.
Для анализа статического и динамического режимов электроприводов используют зависимости моментов от скорости, либо ω.
Зависимости ω(М) и ω( 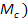 называют механическими характеристиками двигателя и нагрузки соответственно. Механические характеристики двигателя и нагрузки рассматриваемые одновременно позволяют достаточно просто определить координаты, скорость и моменты в установившемся режиме
называют механическими характеристиками двигателя и нагрузки соответственно. Механические характеристики двигателя и нагрузки рассматриваемые одновременно позволяют достаточно просто определить координаты, скорость и моменты в установившемся режиме 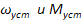 .
.
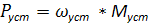
Позволяет определить эти характеристики и установить привода в статическом режиме. Для проектирования электропривода важным этапом является сведение реальной системы к простой модели, состоящей из двигателя, условного редуктора и нагрузки, обладающих определенными моментами, моментами энергии и коэффициентом передачи i и η вида
| Напр(Jн) |
| Ред |
| двиг ( J) |
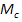
М ω i, η 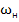
При определенных допущениях в построениях эквивалентной системы по жесткости, зазорам, неизменности моментов энергии во времени для промежуточных валов ( если такие есть) производится пересчет моментов, моментов энергии, нагрузки и всех промежуточных элементов к некоторому основному валу, напряжение к валу двигателя. Пересчет ведется при условии, что в реальной и приведенных системах мощность остается неизменной, т.е. если пренебречь потерями в передаче должно выполняться равенство 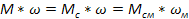 , где
, где 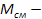 статический момент на валу рабочей машины или механизма и для вращательного движения после пересчета простейшая схема имеет вид. В результате пересчета все параметры приведенные к валу двигателя
статический момент на валу рабочей машины или механизма и для вращательного движения после пересчета простейшая схема имеет вид. В результате пересчета все параметры приведенные к валу двигателя
| J |
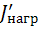
|
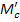
М ω
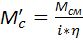 – приведенный момент напряжения,
– приведенный момент напряжения,
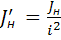 - приведенный момент инерции нагрузки.
- приведенный момент инерции нагрузки.
При преобразовании вращательного движения в поступательное по схеме:
| J |
М ω V
| m |
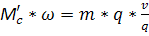 ,
,
где m – масса груза, V – скорость, q – ускорение свободного падения.
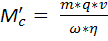 , кинетическая энергия
, кинетическая энергия
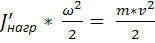 ;
; 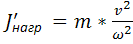 .
.
Дата добавления: 2019-02-08; просмотров: 742;











