Понятие статической устойчивости.

Динамика электропривода имеет важное значение при исследование условий устойчивости электрического привода при нарушении его установившегося значения. При исследовании устойчивости электрических приводов целесообразно разграничить два вида нарушения устойчивости:

а) Когда изменение установившегося режима протекает медленно и роль инерционных масс или индуктивности не значительно.

б) Когда это изменение происходит быстро и нельзя пренебречь влиянием инерционных масс или индуктивностью.

Исследование устойчивости в первом случае относится к области статической устойчивости или саморегулирования, а во втором случае к области динамической устойчивости.

Рассмотрим некоторые вопросы статической устойчивости электрического привода.

Привод находится в равновесии, если при определенной скорости его вращения момент (М_д) равен моменту сопротивления (М_с) рабочей машины М_д=М_с – это равновесие может быть устойчивым, неустойчивым и безразличным.

При устойчивом равновесии под воздействием внешнего фактора (внезапного) нарушившего равновесие, привод вновь возвращается к устойчивому состоянию.

При неустойчивым равновесии скорость привода начинает расти или уменьшаться до полной остановки привода. На границе между устойчивым и неустойчивым равновесием находится безразличное равновесии, при котором привод независимо от нарушения его установившегося равновесия сохраняет свое устойчивое состояния при различных скоростях, но при небольшом диапазоне.

Под статической устойчивостью электрического привода понимается способность его автоматически восстанавливать установившейся режим работы, при его нарушении без помощи регуляторов за счет свойств электрического привода обусловленных механическим характеристикам двигателя и рабочей машины. Статическая устойчивость свойственна не всякому электрическому приводу, поэтому для определения статической устойчивости пользуются критерием статической устойчивости.

2. Критерий статической устойчивости.

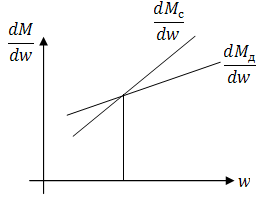
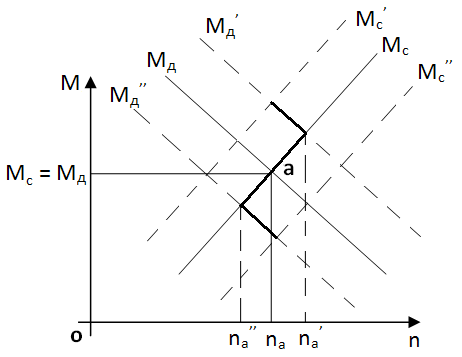Пусть механическая характеристика двигателя и рабочей машины заданы зависимостями М_д=f₁(n); М_с=f₂(n), которые могут не имеет аналитических выражений и быть заданы в виде кривых. Точка пересечения кривых т.а определяет состояние равновесия для которой М_д=М_с, а скорость соответствует некоторому значению n_a.

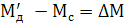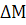Пусть по каким либо причинам механическая характеристика изменилась и заняла положение М_д^’ отличное от М_д, если статический момент (М_с) не изменился, то за счет разности , где – избыточный момент, произойдет изменение скорости до значения М_с^’ при котором М_с и М_д^’ сравняются. Привод достигнет своего нового равновесия. В сторону изменения М_д^’’ процесс аналогичен.

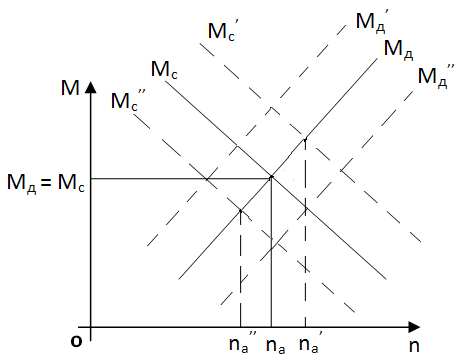
Если кривые движущего момента М_д и М_с поменять местами, то привод становится неустойчивым.

Пусть уравнение движения имеет вид

где М = М_с – М_пр – М_эм

М_пр – внешний момент приложенный к валу электрического двигателя. Например от механического двигателя или за счет запаса кинетической энергии, такой момент на всегда существует и определяется конкретными условиями. Будем считать М_пр=0.

М_эм – электромеханический момент развиваемый двигателем.

М_с – момент нагрузки или статическое сопротивление, которое учитывает статическое трение и все составляющие моменты нагрузки, не зависящие от скорости.

В установившемся режиме w₀=const, значит

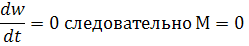
На практике М может быть функцией скорости заданной аналитически или графически. В этом случае выражение (41) справедливо для малых отклонени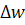й и 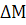от устойчивого состояния определяемого w₀=const.

Функцию 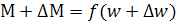разложив в ряд Тейлора, при аналитическом задании и в окрестностях точки w₀ и ограничившись производной первого порядка.

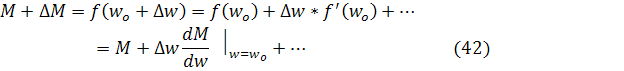
т.к 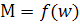, то

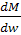– определено в точке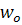

С учетом (43) выражение (41) представляет линейное дифференциальное уравнение первого порядка относительно 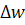, решением которого является выражение вида :

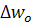– постоянная интегрирования.

При 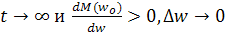это означает, что привод возвращается к своему установившемуся состоянию 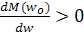означает, что

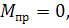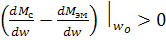Если то или

Выражение (46) и есть критерий статической устойчивости привода, при w =w₀, т.е. для того, чтобы электрический привод с моментом нагрузки М_с=М_д при w =w₀ обладал статической устойчивостью необходимо, чтобы в данной точке (при w =w₀) производная момента нагрузки по скорости была больше произведения момента приводного двигателя по скорости.

Если же показатель степени выражения (44) больше нуля, то привод не обладает статической устойчивостью и 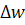растет, при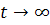

Если же показатель степени выражения (44) равен нулю, т.е 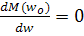то критерий недостаточен ля выявления устойчивости привода.

Другими словами для устойчивости привода необходимо, чтобы механическая характеристика двигателя в точке w_o имела отрицательную производную 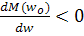, была убывающей по скорости, но основным критерием служит выражение (46). Устойчивость привода возможна и при положительных производных но удовлетворяющих выражению (46).