Устойчивость решения систем дифференциальных уравнений

Решение 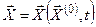системы уравнений вида

,

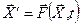(7.19)

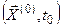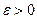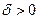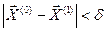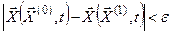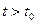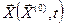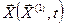соответствующее начальным условиям , называется устойчивым по Ляпунову, если для любого можно найти такое , что из неравенства будет следовать неравенство для всех , где , - решения, соответствующие начальным условиям , .

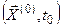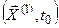Другими словами, система уравнений устойчива, если малое изменение начальных условий не вызывает больших изменений решения.

В общем случае анализ устойчивости дифференциальных уравнений является сложной задачей, однако для систем линейных дифференциальных уравнений критерий устойчивости решений получается достаточно просто.

Поскольку решение системы линейных дифференциальных уравнений представляется в виде (7.17), то каждая неизвестная функция 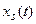есть линейная комбинация экспонент собственных значений, умноженных на время

,

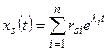(7.20)

где 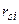- коэффициенты, определяемые начальными условиями и матрицей системы уравнений.

Возьмем для простоты одну экспоненту 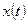= 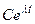и рассмотрим условия, при которых она обеспечивает устойчивое решение. Возможны следующие варианты.

1. l- вещественное положительное число не равное нулю. В этом случае решение апериодически неустойчиво (рис. 7.11, а), поскольку даже при самом малом изменении начального условия (С,0) с увеличением t разность 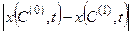может стать сколь угодно большой

2. l - вещественное отрицательное число. 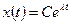, 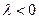. В этом случае решение апериодически устойчиво (рис. 7.11, б).

3. 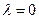. . 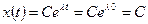Граничный случай, промежуточное состояние между устойчивым и неустойчивым (рис. 7.11, в).

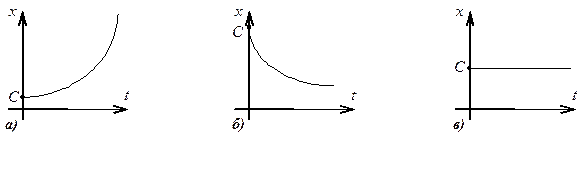Рис. 7.11.Решения ДУ с вещественными собственными числами

4. l - комплексное число.

При решении характеристического уравнения комплексные корни могут появляться только комплексно-сопряженными парами, поэтому в сумме (7.20) имеются члены вида

,

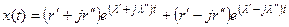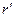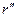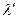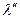где и - вещественная и мнимая части коэффициента r; и - вещественная и мнимая части собственного числа l.

С учетом соотношения 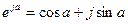последнее выражение может быть преобразовано к виду

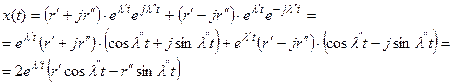
или ,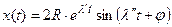

где R - амплитуда колебаний при 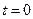, 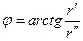- начальная фаза колебаний, величины, определяемые начальными условиями.

Нетрудно видеть, что устойчивость ДУ определяется экспоненциальной составляющей. При этом возможны следующие ситуации.

1. 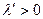. Решение колебательно неустойчиво (рис. 7.12, а).

2. 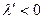. Решение устойчиво, затухание колебательное (рис. 7.12, б).

3. 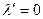. Граничный случай - незатухающие колебания (рис. 7.12, в).

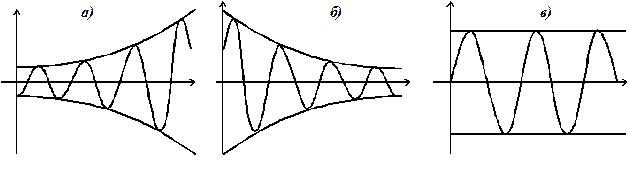Рис. 7.12. Периодическая составляющая

На основании выполненного анализа можно сделать вывод, что решение системы линейных уравнений вида (7.19) будет устойчиво, если все собственные числа матрицы А имеют отрицательные вещественные части.

Пример. Сделать вывод об устойчивости решения дифференциального уравнения

.

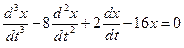Представленному ДУ поставим в соответствие характеристическое уравнение

.

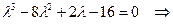
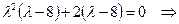
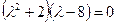Найдем корни характеристического уравнения

; .

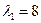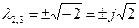Получено три корня, один из которых является положительным и вещественным (данный корень соответствует апериодическому неустойчивому решению, рис. 7.11,а), а два оставшихся - чисто мнимые комплексно-сопряженные корни (соответствуют границе колебательной устойчивости, рис. 7.12, в). Общее решение заданного ДУ является неустойчивым.