Уравнения Лагранжа-Максвелла 2 рода

Уравнения Лагранжа - Максвелла – универсальны и справедливы для любой системы координат. Форма уравнения Лагранжа – Максвелла не зависит от физической природы параметров.

Представим систему уравнений 2-го рода применительно к электромеханической системе в полном объеме

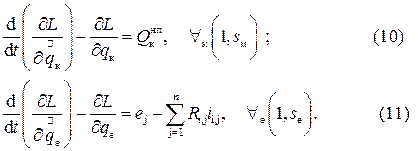
Уравнение (10) справедливо для всех степеней свободы механической подсистемы от 1 до s_м , а уравнение (11) справедливо для всех степеней свободы электрической подсистемы от 1 до s_е.

Эти уравнения записаны на энергетическом уровне.

Для электромеханической системы функция Максвелла имеет вид

L=(T_м+Т_е) - (П_м-П_е), (12)

где Т_м – кинетическая энергия механической подсистемы;

Т_е – кинетическая энергия электрической подсистемы;

П_м – потенциальная энергия механической подсистемы;

П_е– потенциальная энергия электрической подсистемы.

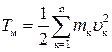– кинетическая энергия для линейного характера поступательного движения, где m – масса объекта,υ – линейная скорость перемещения объекта;

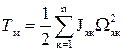– кинетическая энергия для вращательного движения, где J_xк – момент инерции к– ой точки относительно оси, проходящей через центр вращения;

Ω_xк– угловая скорость вращения к– ой точки.

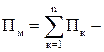сумма потенциальных энергий всех материальных точек.

Кинетическая энергия электрической подсистемы – это энергия магнитного поля подсистемы.

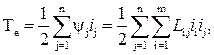(13)

где Ψ_j – потокосцепление; i – ток , j – количество контуров; L_i,j – индуктивность, если i=j, то это собственная индуктивность; если i≠j, то это взаимная индуктивность; i_i, i_j – токи соответствующих контуров.

Потенциальная энергия электрической подсистемы – это энергия электрического поля.

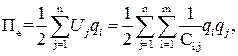(14)

где С_i,j – ёмкость I – го и j – го элементов; q_i , q_j – заряды i – го и j – го элементов.

В выше приведенной системе уравнений Лагранжа – Максвелла используются так называемые обобщенные координаты q, которые однозначно определяют положение или состояние системы.

Это координаты:

q_к – обобщенная координата механической подсистемы.

q_j – обобщенная координата электрической подсистемы.

Обычно в качестве обобщённой координаты выбирается та координата, которая уже не дробится на другие.

Введем также понятие число степеней свободы s:

s_м – число степеней свободы механической подсистемы;

s_e– число степеней свободы электрической подсистемы, определяет количество выделенных независимых контуров.

В уравнениях Лагранжа – Максвелла применяется также понятие «связи». Связи – это условия, определяющие свободу перемещений точек системы.

Связи могут быть кинематическими и аналитическими, представленными в форме

уравнений L=L(x) , M=M(x) , Ψ=Ψ(x) , С=С(x),

где Ψ – потокосцепление , C – ёмкость, М – взаимоиндуктивность, L – индуктивность.

Введенное выше обозначение 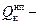означает обобщённые силы, не связанные с потенциальной энергией, т.е. «не потенциальные силы». Размерность обобщённой не потенциальной силы может не совпадать с размерностью силы физической .

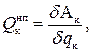(15)

где А_к – элементарная работа, q_к – обобщенная координата механической подсистемы.

δА_к – определяется как работа всех активных сил на возможном перемещении.

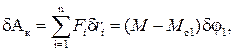(16)

где δr_i– возможные перемещения материальных точек. Возможные перемещения - это перемещения, вызываемые изменениями обобщённых координат.

нп – обобщённые силы, не связанные с потенциальной энергией.

е_j – это ЭДС в независимых координатах.

R_i,j – активные cопротивления в j – ых независимых контурах, по которым протекает соответствующий ток.