Расчетные схемы механической части электропривода. Одномассовая расчетная схема

Элементы, образующие механическую часть ЭП, связаны между собой и оказывают тем самым друг на друга соответствующее воз­действие. Поэтому, анализируя механическое движение того или иного элемента, необходимо учитывать влияние на него других эле­ментов кинематической схемы ЭП. Это достигается соответствую­щим пересчетом входящих в уравнения (31) - (34) сил, моментов, масс и моментов инерции к элементу, движение которого рас­сматривается. Такой расчет в теории ЭП получил название опера­ции приведения, а сами пересчитанные переменные и параметры называют приведенными.

Рассмотрим подробнее операцию приведения и получим соот­ветствующие математические формулы на примере механической части ЭП подъемной лебедки, кинематическая схема которой при­ведена на рис. 3, а [1]. Электродвигатель 1 вращательного движения с моментом инерции J_дв через одноступенчатый редуктор 4 с парой шестерен 5 и 6 приводит во вращение с угловой скоростью Ω_б бара­бан 8 подъемной лебедки, который с помощью троса 9 и крюка 10 поднимает (или опускает) с линейной скоростью υ_и.о груз 11 мас­сой m. На схеме показаны также соединительные механические муф­ты 3 и 7, первая из которых служит шкивом для механического тор­моза 2. Примем допущения, что все элементы приведенной кине­матической схемы являются абсолютно жесткими и между ними от­сутствуют зазоры.

Операцию приведения можно выполнять относительно любого элемента, движение которого подлежит рассмотрению. Обычно в качестве такого элемента выбирают двигатель 1, являющийся ис­точником механического движения. В этом случае сущность опера­ции приведения состоит в том, что реальная схема механической ча­сти ЭП (см. рис. 3, а) заменяется некоторой расчетной (эквивалент­ной) схемой, основой которой является двигатель 1 (см. рис. 3, б), а остальные элементы этой схемы представляются некоторыми пока неизвестными приведенными моментом нагрузки (сопротивления) М_с и моментом инерции J. Такая расчетная схема получила название одномассовой схемы или жесткого приведенного механического звена. Математические соотношения, позволяющие определить М_с и J и тем самым перейти к расчетной схеме, определяются исходя из закона сохранения энергии.

Определение приведенного момента инерции J. Запишем выраже­ния для определения кинетической энергии элементов в реальной (см. рис. 3, а) и расчетной (см. рис. 3, б) схемах и приравняем их друг к другу

, (36)

где J₁ - суммарный момент инерции элементов, вращающихся со скоростью Ω (кроме двигателя), J₂-момент инерции элементов, вра­щающихся со скоростью барабана Ω_б.

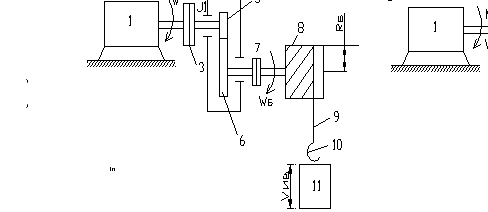
Рис. 3. Кинематическая схема электропривода лебедки

Умножая обе части выражения (36) на 2/Ω², получим

(37)

Отметим, что в (37) отношение

Ω/Ω_б=Z₂/Z₁=i_р – соответ­ственно числа зубцов шестерен 6 и 5 является передаточным отно­шением редуктора, а отношение υ_и.о/Ω= Ω_бR_б /Ω= R_б /i_р=ρ пред­ставляет собой так называемый радиус приведения (ρ) кинематичес­кой схемы между исполнительным органом (крюком 10) и валом двигателя. С учетом этого окончательно получим

J = J_дв + J₁+ J₂/(i_р)²+mρ² . (38)

Из (38) вытекает общее правило: для расчета J следует моменты инерции вращающихся элементов разделить на квадрат передаточ­ного числа кинематической схемы между этими элементами и ва­лом двигателя, а массы поступательно движущихся элементов ум­ножить на квадрат радиуса приведения и полученные результаты расчета сложить с моментами инерции двигателя и элементов, вра­щающихся с его скоростью.

Приведение момента нагрузки М_с к валу двигателя

При подъеме груза к исполнительному органу от ЭП должна быть подведена ме­ханическая мощность

Р_и.о=F_и.оυ_и.о=mgυ_{и. о,}

где g – ускорение силы тяжести; F_{и. о}– усилие, развиваемое исполни­тельным органом.

Учитывая с помощью КПД потери мощности в кинематической цепи, запишем баланс мощности нагрузки ЭП в реальной и расчет­ной схемах:

М_сΩ=mgυ_и.о/η, (39)

где η – результирующий КПД кинематической схемы ЭП;

В рассматриваемом примере η = η_рη_б, где η_р и η_б – КПД соответственно редуктора 4 и барабана 8.

Разделив обе части (39) на Ω, находим

М_с=mgυ_и.о/(ηΩ)=F_{и. о}ρ/η. (40)

Если исполнительный орган совершает не поступательное, а вра­щательное движение, то

М_сΩ = М_{и. о}Ω_{и. о}/η, (41)

где М_{и. о}, Ω_{и. о} – соответственно момент нагрузки и скорость испол­нительного органа, а приведенный момент нагрузки

М_с=М_{и. о}/(ηi_р). (42)

При спуске груза запасенная в нем потенциальная энергия пере­дается к двигателю, частично расходуясь на преодоление потерь в кинематической схеме. В силу этого к двигателю поступает мень­шая энергия и тогда при поступательном движении

M_c=F_{и. о}ρη, (43)

а при вращательном движении

М_с = М_и.оη/i_р. (44)

Отметим, что приведенный момент нагрузки М_с также называ­ют статическим моментом или моментом сопротивления.

При использовании в ЭП двигателя поступательного движения, пока еще редко применяемого, приведение осуществляется по тем же принципам.

Выполнение операции приведения и переход тем самым к рас­четной схеме рис. 3, б позволяет раскрыть левую часть уравнения (44). В общем случае входящие в него моменты двигателя М и сопротивления М_с могут иметь как положительные, так и отрица­тельные знаки:

±М ±М_с =JdΩ/dt. (45)

Правило, по которому определяются эти знаки, следующее: если направление действия момента совпадает с направлением скорос­ти, то такой момент считается положительным, и наоборот.

В наиболее типичном для ЭП случае двигатель создает движу­щий момент, а исполнительный орган – момент сопротивления дви­жению. Тогда (45) принимает следующий вид:

M-M_c=JdΩ/dt. (46)

Левая часть уравнения (46), представляющая собой разность моментов двигателя и нагрузки и определяющая условия ускоре­ния или замедления движения, в теории электропривода получила название динамического момента, М_дин = М - М_с.

Задача 1. Выполнить операцию приведения в случае подъема груза при следующих параметрах кинематической схемы (см. рис. 3, а) [5]: J_дв = 0,1 кг•м²;

J₁= 0,02 кг•м² ; J₂ = 2 кг•м² ; m = 1000 кг; R_б = 1,15 м; υ_и.о = 0,9 м/с; Z₁ = 14; Z₂ = 86; η_р = 0,97; η_б= 0,96.

Передаточное число редуктора

i_р = Z₂/Z_l =86/14 = 6,14;

радиус приведения кинематической схемы

ρ = R_б/i_р = 0,15/6,14 = 0,024 м;

момент инерции

J = J_дв + J₁+ J₂ /(i_р)²+ mρ² = 0,1 + 0,02 + 2/6,14² +1000• 0,024² = 0,8 кг•м²;

По (40) рассчитаем приведенный момент нагрузки

М_с=(mgρ)/(η_рη_б)=(1000•9,81•0,025)/(0,97•0,96)=263 Нм.

Задача2. Для рассмотренного выше примера определить J и М_с в случае спуска груза, приняв те же значения параметров и КПД кинематической схемы.

Рис. 4. Кинематическая схема лифта

Задача 3. Требуется записать в общем виде формулы для определения J и М_c, если заданы следующие параметры кинематичес­кой схемы лифта, схема механической части которого приведена на рис.4:

– грузоподъемность лифта m_г кг;

– скорость дви­жения кабины 6 υ_{и. о} м/с;

– масса кабины m_к кг;

– масса противовеса 8 m_пв кг;

– диаметр канатоведущего шкива 5 d_{к. ш} м;

– передаточное число редуктора 4 i_р ;

– КПД механической части η_{м. ч};

– длина троса 7 L_т м;

– масса погон­ного метра троса m_т кг/м;

– моменты инерции элементов, вращающихся со скоростями Ω и Ω_к.ш, соответственно J₁ и J₂, а также момент инерции двигателя 2 J_дв.

Двигатель 2 связан с тормозом 1 и через муфту 3 с редуктором 4.

Задача 4. Для кинематической схемы механической части ЭП тележки мос­тового крана, приведенной на рис. 5, необходимо определить J и M_с при следующих исход­ных данных:

– скорость перемещения тележки υ_ио= 0,8 м/с;

– диаметр ходовых ко­лес ХК d_{x. к} = 0,6 м;

– общая масса тележки с грузом m_т = 8 500 кг, сила сопротивления движению тележки F_{и. о}= 120 000 Н;

– J_дв = 0,1 кг•м²; J₁= 0,15 кг•м²; J₂ = 0,01 кг•м²; J₃ = 0,05 кг•м²; Z₁ = 20; Z₂ = 79;

Z₃ = 16; Z₄ = 83;

– КПД одной шестеренчатой пары η_п=0,97.

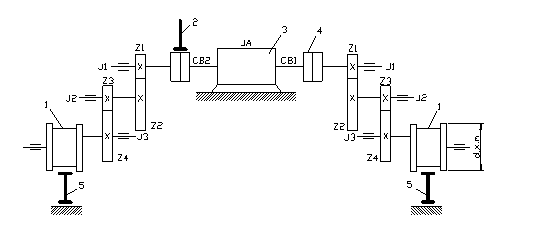
Рис. 5.Кинематическая схема электропривода тележки мостового крана: 1 – ходовые колеса; 2 – тормоз; 3 – двигатель; 4 –муфта; 5 – рельс.