Многомассовые расчетные схемы

Реальные кинематические схемы ЭП содержат упругие элемен­ты (элементы конечной жесткости), между которыми могут суще­ствовать зазоры [1]. Так, например, в схеме рис. 3, а таким упругим элементом является трос 9, на котором подвешивается груз. При значительной протяженности к упругим элементам относят и со­единительные валы. Зазоры в этой схеме могут существовать в со­единительных муфтах 3 и 7, а также в шестеренчатом зацеплении и подшипниках.

Наличие упругих элементов и зазоров усложняет расчетную схе­му механической части ЭП, превращая ее в многомассовую. Так, если в расчет принимать упругость одного элемента и зазоры при этом не учитывать, то выполнение операции приведения позволит представить механическую часть ЭП в виде так называемой двухмассовой расчетной схемы, изображенной на рис. 6 [3].

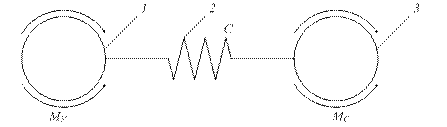
Рис. 6.Двухмассовая расчетная схема

В этой схеме упругий элемент 2 с коэффициентом жесткости с соединяет две массы 1 и 3 с моментами инерции соответственно J₁ и J₂ . Первая из масс, которая включает в себя массу движущейся ча­сти двигателя и жестко связанных с ним элементов кинематической схемы, вращается со скоростью Ω₁, а другая масса, включающая в себя массу исполнительного органа и жестко связанных с ним эле­ментов, – со скоростью Ω ₂. К первой массе приложен при этом мо­мент двигателя М и упругий момент М_у, а ко второй – упругий мо­мент и момент нагрузки М_с. Движение двухмассовой системы опи­сывается в этом случае совокупностью следующих уравнений:

М - M_y=J₁dΩ/dt;

М_у - М_с=J₂dΩ/dt;

М_у=с(φ₁- φ₂),

где φ₁ и φ₂ – углы поворота соответственно первой и второй масс;

с – коэффициент жесткости, определяемый материалом и геомет­рическими размерами упругого элемента 2. Приведение коэффициента жесткости к валу двигателя упруго­го стержня осуществляется по формуле

с = с₁ ρ², (47)

а к валу двигателя упругого вала (оси) вращения – по формуле

с = с₂/(ι_р)², (48)

где с₁ и с₂ - соответственно коэффициенты жесткости упругого стер­жня, Н/м , и упругого вала, Нм.

При параллельном соединении нескольких упругих элементов с коэффициентами жесткости с₁, c₂, с₃,... эквивалентная жесткость

с_экв = с₁ + с₂+ с₃ +..., (49)

а при их последовательном соединении

1/с_экв=1/с₁+1/с₂+1/с₃+.... (50)

При учете упругости двух или более элементов расчетная схема получается соответственно трехмассовой, четырехмассовой и т.д. Многомассовые расчетные схемы получаются и в том случае, ког­да необходимо принять во внимание зазоры в кинематической схе­ме ЭП. Движение элементов в многомассовых схемах более слож­ное и многообразное [2], и для его анализа требуется применение вычислительной техники.

Задача 5. Для механической части ЭП из задачи 1 (см. рис. 3, а) полу­чить расчетную схему с учетом упругости троса, коэффициент жесткости с кото­рого принять равным 105 Н/м. Массу троса не учитывать.

Упругий элемент (трос) разделяет поднимаемый груз и остальную механи­ческую часть ЭП. Так как условием задачи предусматривается учет только од­ной упругости, то расчетная схема будет двухмассовой (см. рис. 6).

Тогда момент инерции первой массы

J_I =J_дв +J₁ +J₂/ι²_р =0,1 + 0,02+ 2/6,14² =0,175 кг•м², а момент инерции второй

массы J_II

J_II=mρ²=1000•0,025²=0,625 кг•м².

Задача 6. Для кинематической схемы тележки крана, приведенной на рис.4, получить в общем виде расчетную схему при учете упругости валов, имеющих коэффициенты жесткости с_в1 и с_в2.

2.5. Установившееся движение электропривода и его устойчивость [1]

Для расчетной одномассовой схемы, приведенной на рис. 3, б, установившееся механическое движение ЭП будет определяться ра­венством моментов двигателя и нагрузки, т.е. условием М = М_с. Проверка выполнения этого условия может производиться анали­тически или с помощью так называемых механических характерис­тик двигателя и исполнительного органа.

Механической характеристикой двигателя называется зависи­мость его скорости от развиваемого момента Ω(М) (для враща­тельного движения) или усилия υ(F) (для поступательного движе­ния). Различают естественную и искусственную характеристики двигателей.

Естественная характеристика двигателя (она у него единствен­ная) соответствует основной (паспортной) схеме его включения и номинальным параметрам питающего напряжения. Естественные механические характеристики двигателей вращательного движения приведены на рис. 7, а (1–4) – соответственно синхронного, по­стоянного тока с независимым возбуждением, асинхронного и постоянного тока с последовательным возбуждением). На естественной характеристике располагается точка номинального (паспортного) режима работы двигателя с координатами Ω _ном, М_ном.

Если включение двигателя происходит не по основной схеме, или в его электрические цепи включены какие-либо дополнительные электротехнические элементы (резисторы, реакторы, конденсато­ры), или двигатель питается напряжением с неноминальными параметрами, то его характеристики будут называться искусствен­ными.

Таких характеристик у двигателя может быть сколь угодно много. Поскольку эти характеристики получают с целью регулиро­вания переменных (координат) двигателя – тока, момента, скорос­ти, положения, то они иногда называются регулировочными. Ис­кусственные характеристики двигателя и способы их получения подробно рассматриваются далее.

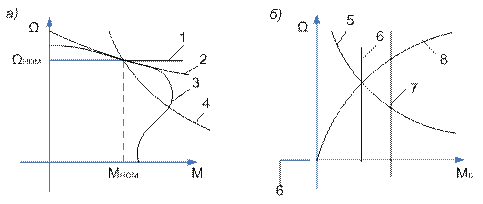
Рис. 7.Механические характеристики двигателей (а) и исполнительных органов (б): 1-4 – соответственно синхронного, постоянного тока с независимым возбуждением, асинхронного и постоянного тока с последовательным возбуждением; 5 – механизма главного двигателя металлообрабатывающего станка; 6 – транспортера, механизма подачи станка; 7 – подъемного механизма; 8 – вентилятора, дымососа, компрессора и центробежного насоса

Механической характеристикой исполнительного органа(ИО)называ­ется зависимость скорости его движения от усилия или момента на нем, т.е. Ω _ио(М_ио) при вращательном движении и υ_и.о(F_и.о) при по­ступательном движении. В результате операции приведения эти ха­рактеристики преобразуются в зависимость вида Ω (М_с), где Ω – ско­рость двигателя, а М_с – приведенный к его валу момент нагрузки (сопротивления). Механические характеристики некоторых испол­нительных органов приведены на рис. 7, б (5 – механизма главно­го движения металлообрабатывающего станка; 6 – транспортера, механизма подачи станка; 7 – подъемного механизма; 8 – вентиля­тора, дымососа, компрессора и центробежного насоса). Отметим, что реальные механические характеристики исполнительных орга­нов более сложны по своему виду и обычно представляют собой сочетание показанных на рис. 7, б зависимостей.

На практике часто в качестве механических характеристик ИО используют зависимости момента от скорости М=f(Ω). Механические характеристики подавляющего большинства ИО можно представить единой формулой

М=М_о +(М_N-М_о)(Ω/Ω_о)^х (51)

Показатель степени х в зависимости от характера нагрузки может принимать значения х=0; 1; 2; (-1).

При х=0 момент ИО постоянный и не зависит от скорости М=М_N=const,

она изображена на рис. 8 прямой 1. В технике эту характеристику называют характеристикой типа «сухое трение».

При х=1 момент ИО прямопропорционален скорости вращения. Эту характеристику называют характеристикой типа «вязкое трение», она изображена на рис. 8 прямой 2.

При х=2 момент ИО пропорционален квадрату скорости вращения. Эту характеристику называют вентиляторной характеристикой, она изображена на рис. 8 кривой 3.

При х=-1 момент ИО обратнопропорционален скорости вращения, а произведение момента на скорость остается постоянным, поэтому эту характеристику называют характеристикой постоянной мощности Р=const, она изображена на рис. 8 кривой 4.

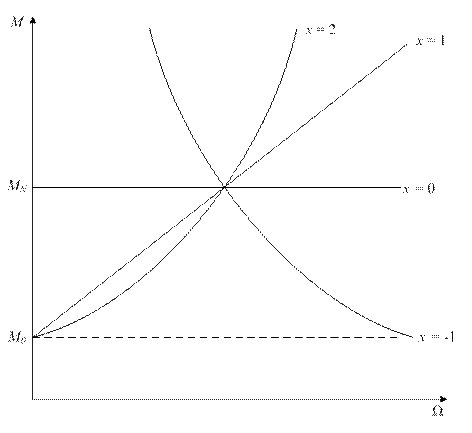
Рис.8. Механические характеристики исполнительных механизмов

По характеру действия моменты нагрузки М_с делятся на актив­ные и реактивные.

Активные моменты имеют постоянное, не за­висящее от скорости направление своего действия и создаются так называемыми потенциальными силами – силами притяжения Зем­ли (характеристика 7 нарис. 7, б), силами упругой деформации и др.

Реактивный момент, характеристика которого соответствует за­висимости 6 на рис. 7, б, создается в основном силами трения, он всегда противодействует движению и поэтому изменяет свой знак с изменением направления скорости движения.

Количественно механические характеристики двигателя и испол­нительного органа оцениваются жесткостью β, определяемой как

β = dM/dΩ ≈ΔМ/ΔΩ. (52)

Используя этот показатель, можно оценить характеристику син­хронного двигателя 1 как абсолютно жесткую (β=∞, характерис­тику асинхронного двигателя 3 – как имеющую переменную поло­жительную и отрицательную жесткости, а характеристику подъем­ного механизма 7 – как имеющую нулевую жесткость (β = 0) и т.д.

Введенное понятие механических характеристик позволяет гра­фически выполнить проверку условия установившегося движения и найти его параметры. Для этого в одном и том же квадранте со­вмещаются характеристики двигателя 1 и исполнительного органа 2, как это показано на рис. 9. Точка А пересечения этих характе­ристик, в которой моменты двигателя и исполнительного органа равны, и будет соответствовать установившемуся движению со ско­ростью Ω _уст и моментом М_уст.

Аналитический способ для такой проверки применяется в тех слу­чаях, когда механические характеристики двигателя и нагрузки за­даны в виде двух уравнений, совместное решение которых при ус­ловии М = М_ст дает искомое значение Ω _уст. Подстановка этого значения скорости в любое из двух уравнении механических характе­ристик позволяет получить значение установившегося момента.

По виду механических характеристик двигателя и исполнительно­го органа можно определить будет ли устойчивым установившееся движение ЭП. Под устойчивостью понимается свойство системы «двигатель – исполнительный орган» поддерживать движение со скоростью Ω_уст или с минимально возможными отклонениями от нее. Рассмотрим способ определения устойчивости движения с помощью механичес­ких характеристик (см. рис. 9).

Предположим, что по какой-то причине скорость ЭП повыси­лась до уровня Ω₁. Выясним, что будет происходить со скоростью, если вызвавшая ее изменение причина исчезнет. Из характеристик двигателя и исполнительного органа видно, что при скорости Ω ₁ момент нагрузки М_с1 больше момента двигателя M₁ т.е. М₁ < М_с1. Тогда в соответствии с (46) в системе «двигатель – исполнитель­ный орган» будет действовать отрицательный динамический мо­мент. Начнется процесс торможения (dΩ /dt < 0), который закончит­ся при скорости Ω _уст.

Рассмотрим теперь положение, при котором кратковременное возмущение вызвало снижение скорости до уровня Ω ₂ < Ω _уст. В этом случае М₂ > М_с2 и под действием уже положительного динамичес­кого момента скорость начнет возрастать, пока не достигнет уров­ня Ω _уст. Таким образом, система «двигатель –исполнительный орган» с приведенными на рис. 9 механическими характеристи­ками обладает свойством возвращаться к скорости установивше­гося движения при возможных отклонениях от нее, т. е. движение в такой системе является устойчивым.

Проверка на устойчивость движения может быть выполнена также аналити­чески с использованием понятия жест­кости характеристик. Движение будет устойчиво при выполнении условия

β- β_с<0 или β< β_с,

где β и β_с – соответственно жесткости ме­ханических характеристик двигателя и исполнительного органа.

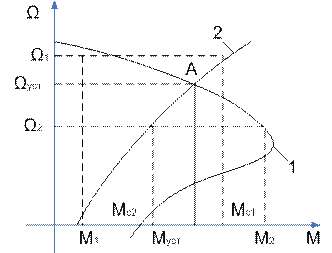
Рис. 9.Графики для определения скорости установившегося движения и статической устойчивости работы электропривода

Задача 7. Уравнения двигателя и исполнительного органа рабочей ма­шины имеют соответственно вид Ω= 300 - 3М и М_с = 30 + 2Ω. Определить ана­литически установившиеся скорость Ω _уст и момент М_уст.

Используя условие установившегося движения М = М_ст, запишем

30 + 2Ω _уст = (300 - Ω _уст)/3, откуда Ω _уст = 30 рад/с.

Подставляя полученное значение скорости в любое из двух уравнений, по­лучим значение установившегося момента М_уст = 90 Нм.

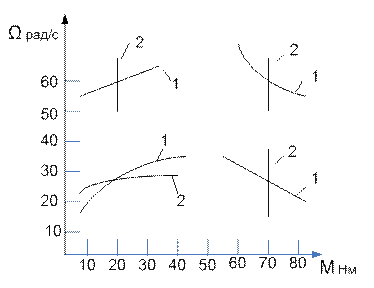
Рис.10. Механические характеристики различных двигателей и исполнительных органов для определения установившейся скорости и статической устойчивости ЭП

Задача 8. На рис. 10 изображены различные механические характеристи­ки двигателя 1 и исполнительного органа 2. Определить графически во всех случаях скорость установившегося движения, жесткость характеристик в обла­сти точки их пересечения и устойчивость установившегося движения ЭП.