Вывод уравнений динамики электрического привода постоянного тока

На рис.2 приведена схема включения двигателя постоянного тока с независимым возбуждением к источникам постоянного напряжения цепи обмотки якоря и цепи обмотки возбуждения. Якорь машины механически связан с нагрузкой.

Необходимо построить математическую модель ЭП на базе ЭД постоянного тока

с независимым возбуждением.

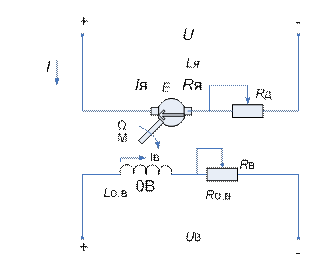
Рис.2. Схема включения ДПТ НВ: U_я – напряжение цепи обмотки якоря; U_в – напряжение цепи обмотки возбуждения; R_д – добавочное сопротивление цепи обмотки якоря; R_в – сопротивление цепи обмотки возбуждения; L_я , L_в– индуктивность обмотки якоря и обмотки возбуждения соответственно; M_дв, M_нг– момент развиваемый двигателем и статический момент нагрузки; Ω – угловая скорость вращения вала двигателя; Е –ЭДС обмотки якоря; I – ток цепи обмотки якоря; I_в– ток цепи обмотки возбуждения.

Примем допущение – соединение вала ЭД с нагрузкой – абсолютно жесткое, трение в подшипниках отсутствует. Механическая подсистема – здесь ротор ЭД, соединенный с нагрузкой.

Установим, что число степеней свободы механической подсистем s_м=1, поскольку система может совершать лишь одно вращательное движения.

Число степеней свободы электрической подсистемы s_е=2 и включает в себя электрическую цепь обмотки якоря и электрическую цепь обмотки возбуждения.

Определим обобщённые координаты системы.

В качестве обобщенной координаты механической подсистемы q₃ выбираем угол поворота вала ЭД q₃=φ .

В качестве обобщенных координат электрической подсистемы выбираем электрический заряд цепи якоря q₁ =q_я и электрический заряд цепи возбуждения q₂ =q_в.

Кинетическая энергия механической подсистемы Т_м=(1/2)JΩ², где

J=J_я+J_н^′ - суммарный момент инерции механической подсистемы, включающий в себя момент инерции ротора двигателя J_я и приведенный к валу двигателя момент инерции нагрузки J_н^′;

Так как 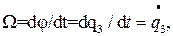то

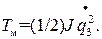(17)

Кинетическая энергия электрической подсистемы

Т_е=(1/2) L_яi_я²+ (1/2 )L_вi_в². (18)

Так как

;

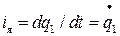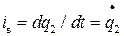, то

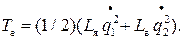
(19)

Уравнения Лагранжа- Максвелла для рассматриваемой системы.

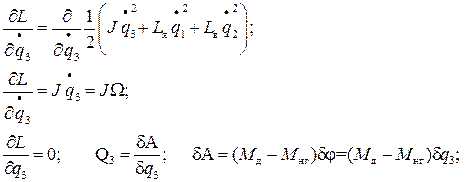
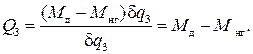(20)

Перейдём теперь к электрической подсистеме.

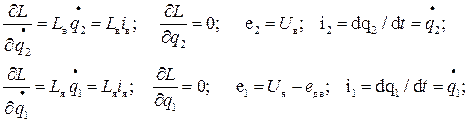
Для механической подсистемы s_к=1:

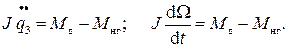(21)

Уравнение (21) называется уравнением движения ЭП.

Отметим, что уравнение (21) выведено из допущения постоянства момента инерции при отработке движения исполнительного органа рабочей машины.

Для электрической подсистемы s_e=2:

- цепь обмотки возбуждения i=2:

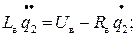
- цепь обмотки якоря i =1:

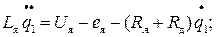(22)

Окончательно уравнения электропривода постоянного тока для динамических режимов

L_яdi_я/dt +i_я(R_я +R_д)= U_я -e_я ; (23)

L_вdi_в/dt +i_вR_в=U_в; (24)

JdΩ/dt= M_дв -M_нг ; (25)

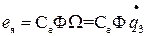; (26)

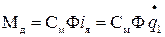; (27)

;

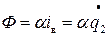M_нг=M(Ф; Ω; p; t …).

Для установившегося режима работы привода di_я/dt=0, di_в/dt=0, dΩ/dt=0 и уравнения (23), (25), (26) приобретают вид

U_я =Е_я+i_я(R_я +R_д); (28)

M_дв =M_нг =С_мФi_я; (29)

Е_я= С_еФΩ; (30)

Ф=const.

Далее рассмотрим механическое движение исполнитель­ных органов рабочих машин и элементов ЭП в установившемся и неустановившемся (переходном) режимах.

Вопросы для самоконтроля

1. Дайте пояснения понятиям «обобщенная координата», «степень свободы», «функция Максвелла».

2. Приведите выражения кинетической энергии механической и электрической подсистем ЭП.

3. Приведите выражения потенциальной энергии механической и электрической подсистем ЭП.

4. Приведите уравнение равновесия напряжения цепи обмотки якоря.

5. Приведите уравнение равновесия напряжения цепи обмотки возбуждения.

6. Приведите выражение уравнения движения ЭП.

2.2. Полные уравнения движения электропривода [1]

В механическом движении участвуют подвижная часть электро­двигателя (ротор или якорь), элементы механического передаточ­ного устройства и исполнительный орган. Совокупность этих эле­ментов называют механической частью ЭП.

Движение любого элемента механической части ЭП (или испол­нительного органа рабочей машины) подчиняется известным из кур­са физики законам механики. Полные уравнения движения ЭП учитывают как изменения скорости, так и изменения момента инерции (при вращательном характере движении) или изменение массы (при поступательном характере движения).

Поступательное и вращательное дви­жения описываются соответственно следующими полными уравнениями:

где ∑F и ∑M – соответственно совокупность сил и моментов, дей­ствующих на элемент;

m и J – соответственно масса и момент инер­ции элемента;

t – время, Ω и υ – соответственно угловая и линейная скорости движения элемента.

Уравнения движения по своему характеру являются дифференци­альными, поскольку содержат производные скорости, массы и мо­мента инерции. В большинстве случаев масса и момент инерции эле­ментов при движении не изменяются, их производные оказываются равными нулю и уравнения (31) и (32) упрощаются:

∑F = mdυ/dt = ma; (33)

∑M = JdΩ/dt = Je, (34)

где a = dυ/dt и e=dΩ/dt соответственно ускорения при поступа­тельном и вращательном движениях.

Обратим внимание, что уравнение (34) при принятых допущениях полностью совпадает с выведенным выше уравнением (21).

Уравнения (33) и (34) отражают известный закон механики: ус­корение движения механического элемента (тела) пропорциональ­но алгебраической сумме действующих на него сил (моментов) и обратно пропорционально его массе (моменту инерции).

Если

dυ/dt =dΩ/dt = 0, то

∑F =0; ∑M =0 (35)

и элемент движется с постоянной скоростью или находится в состоянии покоя.

Другими словами, элемент будет двигаться с неизменной скоро­стью (или будет неподвижным), если сумма сил или моментов, к нему приложенных, будет равна нулю. Такое движение называют установившимся.

При ∑F > 0 или ∑М > 0 элемент будет двигаться с ускорени­ем, а при ∑F < 0 или ∑M < 0 – с замедлением. Условия (35) ис­пользуются для определения параметров установившегося механи­ческого движения.