Матричное представление антагонистической игры

Пусть заданы множества стратегий {A_i}, i =1,… m, и {B_j}, j =1,…,n, игроков A и B соответственно, а также матрица выигрышей A = ||a_ij||, i =1, …, m, j =1, …, n, где элемент a_ij – выигрыш игрока A в ситуации, когда он выбирает стратегию A_i, а игрок B – стратегию B_j. Такая игра G(m´n)может быть представленав матричной форме (и называется матричной игрой) в виде таблицы (табл. 3.1).

Таблица 3.1

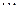
Bj Ai	B1		Bj		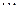Bn
A1	a11		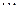a1j		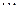a1n
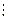
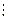
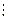
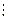
Ai	ai1		aij		ain
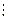
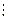
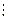
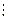
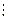
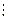
Am	am1		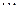amj		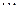amn

В качестве иллюстрации снова рассмотрим игру из примера 1 п. 2.1 для случая неполной информации, т.е. когда игроку B не сообщается о выборе игрока A.У игроков A и B имеется по две стратегии: A₁и A₂ – выбрать 1 или 2 соответственно, B₁и B₂– выбрать 2 или 3 соответственно. Данная игра G(2´2)в матричной форме представлена табл. 3.2.

Таблица 3.2

Bj Ai
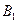
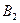
A1		–5
A2	–5

Для случая, когда игроку B известно о выборе игрока A (т.е. игра с полной информацией), получаем игру G(2´4),матричная форма которой представлена табл. 3.3.

Таблица 3.3

Bj Ai
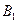
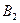
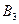
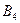
A1		–5		–5
A2	–5			–5

У игрока B добавились еще две стратегии: B₃ – отвечать стратегией с тем же номером, что выбрал игрок A (т.е. B₁на A₁ и B₂на A₂) и B₄ – отвечать стратегией с номером, отличным от выбора игрока A (т.е. B₂ на A₁ и B₁на A₂).