Поиск решения на дереве игры

Общие замечания

Дерево игры может быть построено, используя известные методы полного перебора («в глубину», «в ширину», комбинированный) или сокращенного перебора, выполняемого с использованием некоторой оценочной функции (точной или приближенной, эвристической) [7, 8].

Определение 2.2. Алгоритм поиска решения называется допустимым, если он оканчивает свою работу построением оптимального решения (оптимального пути к цели).

Определение 2.3.Допустимыйалгоритм поиска решения называется оптимальным, если он при поиске решения анализирует (раскрывает) минимальное число вершин.

Примером допустимого (но, конечно, не оптимального) алгоритма является алгоритм, построенный на основе полного перебора. Эвристические алгоритмы, использующие при поиске решения методы сокращенного перебора на основе эвристических функций, как правило, не являются допустимыми, т.е. эти алгоритмы не гарантируют в общем случае нахождение оптимального решения. Преимуществом эвристических алгоритмов являются существенно меньшие затраты вычислительных ресурсов (времени вычислений и памяти) по сравнению с алгоритмами, основанными на полном переборе.

Нильсон Н. (Nilsson N.) в своей классической работе по искусственному интеллекту [7] доказал теорему, определяющую требования к эвристической функции, чтобы алгоритм поиска решения, построенный на ее основе, был допустимым. К сожалению, проверка выполнимости этого требования, в свою очередь, является сложной и обычно практически нереализуемой задачей.

Рассмотрим два универсальных метода сокращенного перебора на дереве игры – метод максимина (максиминный метод) и метод a-b отсечений.

Метод максимина

Суть метода заключается в следующем. Имеется два игрока – A (MAX), задачей которого является максимизация платежа (своего выигрыша), и B (MIN), который, естественно, заинтересован в минимизации этого платежа (своего проигрыша).

Реализуется процедура, результатом выполнения которой является определение наилучшего относительно оценочной функции первого хода игрока A.

Процедура включает следующие шаги.

1. Строится полное поисковое дерево на максимально возможную с учетом вычислительных ресурсов (времени счета и памяти) глубину, при условии равенства числа ходов у обоих игроков.

2. Концевые вершины дерева взвешиваются значениями оценочной функции.

3. Совершается обратное движение по дереву от концевой к начальной вершине с пересчетом значений оценочной функции и итоговым выбором первого хода игрока A, максимизирующего это значение.

Далее осуществляется переход в вершину, соответствующую выбранному ходу, и вся процедура повторяется уже для игрока B, с тем только отличием, что игрок B заинтересован в минимизации значения оценочной функции.

Описанная процедура поочередно применяется для игроков A и B до завершения игры (партии).

Алгоритм поиска на основе метода максимина будет допустимым, если используется точная оценочная функция, и эвристическим, если оценочная функция является эвристической.

Рис. 2.2 иллюстрирует данный метод. Цифры у промежуточных вершин являются пересчитанными для этих вершин значениями оценочной функции. В результате выполнения процедуры будет рекомендовано игроку A в качестве первого хода выбрать переход к вершине S₁ с максимальным значением оценки.

Существенный недостаток метода максимина, следствием которого являются чрезмерно большие затраты вычислительных ресурсов, что, в свою очередь, сокращает глубину построения дерева, заключается в разделении этапов построения дерева и оценки вершин. Усовершенствованием данного метода является метод a-b отсечений, согласно которому отсечение неперспективных вершин производится непосредственно в процессе построения дерева игры.

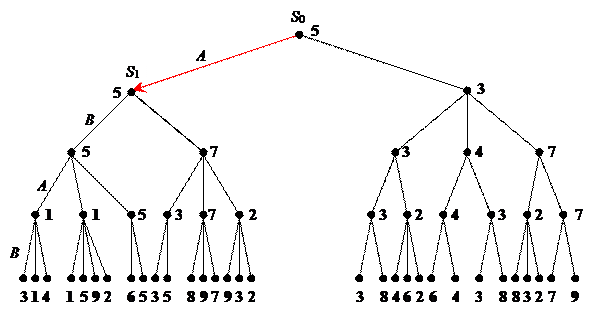
Рис. 2.2. Дерево игры для метода максимина