Смешанные стратегии

В случае отсутствия седловой точки, в качестве решения игры используются так называемые смешанные стратегии

,

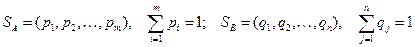где p_i и q_j – вероятности выбора стратегий A_i и B_j игроками A и B соответственно. Решением игры в данном случае является пара оптимальных смешанных стратегий (S_A^*, S_B^*), максимизирующих математическое ожидание цены игры (средний выигрыш).

Теорема 3.2[6]. Любая антагонистическая игра имеет хотя бы одно оптимальное решение, т.е., пару в общем случае смешанных стратегий (S_A^*, S_B^*), дающих игроку А устойчивый выигрыш, равный цене игры V,α ≤ V ≤ β.

Чистую стратегию можно рассматривать как частный случай смешанной стратегии, когда одна вероятность имеет единичное значение, а все остальные – нулевое.

Рассмотрим матричную игру G(m´n), не имеющую седловой точки, для которой необходимо найти решение – пару оптимальных смешанных стратегий S_A =(p₁, p₂, …, p_m)и S_B =(q₁, q₂, …, q_n) и соответствующую цену игры V.

Предварительно следует попытаться упростить матрицу игры. Для этого вводятся отношения предпочтения (доминирования) и безразличия (дублирования) на множестве стратегий.

Определение 3.3:

· стратегия A_i предпочтительнее стратегии A_k (доминирует A_k) (обозначается 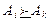), если все выигрыши, указанные в i-й строке матрицы игры, не меньше соответствующих выигрышей k-й строки, или формально ;

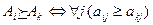· стратегии A_i и A_k находятся в отношении безразличия (дублирования) (обозначается A_i»A_k), если все выигрыши, указанные в i-й строке матрицы игры, совпадают с соответствующими выигрышами k-й строки, или формально ;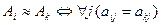

· стратегия B_j предпочтительнее стратегии B_r (доминирует B_r) (обозначается 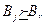), если все выигрыши, указанные в j-м столбце матрицы игры, не меньше соответствующих выигрышей r-го столбца, или формально ;

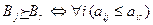· отношение безразличия для стратегий игрока B вводится аналогично игроку A, т.е. .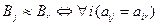

Можно доказать следующую лемму [5].

Лемма 3.2. Для игры G(m´n)число активных стратегий игроков равно min{m,n}. Другими словами, если, например, m>n, то в оптимальной стратегии S_A =(p₁, p₂, …, p_m) игрока A будет не более n отличных от нуля вероятностей p_i.

Таким образом, предварительным этапом решения матричной игры является ее упрощение, т.е. удаление из матрицы доминируемых и дублируемых стратегий.

Рассмотрим данный этап на примере матричной игры G(5´5), представленной табл. 3.7.

Таблица 3.7

Bj Ai	B1	B2	B3	B4	B5
A1
A2
A3
A4
A5

 

Так как справедливы соотношения 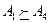, , 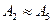, , 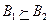, 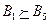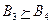то удалим доминируемые и дублируемые стратегии A₄, A₅, B₂, B₄, B₅.

В полученной матрице снова проведём удаление, так как 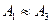. Получим упрощенную игру G(2´2), представленную табл. 3.8.

Таблица 3.8

Bj Ai	B1	B3
A1
A2

 

Нетрудно убедиться, что данная игра не имеет седловой точки и необходимо искать решение в смешанных стратегиях.

После упрощения игры следующим (основным) этапом является поиск оптимального решения в виде смешанных стратегий (S_A, S_B), применяя точные или приближенные методы.

Метод Лагранжа

Метод Лагранжа относится к точным методам решения матричных игр G(m´m), т.е. имеющим квадратные матрицы (или приведенные к такому виду после упрощения).

Допустим, что игрок A использует смешанную стратегию S_A =(p₁, …, p_m), а игрок B отвечает своей чистой стратегией B_i (i =1, 2, …, m). Цена игры в таком случае равна 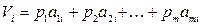. Если же игрок B также будет применять смешанную стратегию S_B =(q₁, …, q_m), то итоговая цена игры будет равна

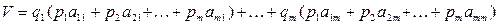. (3.1)

Для нахождения оптимального решения необходимо максимизировать значение V при ограничениях .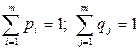

Составим функцию Лагранжа L = V + l₁(p₁ + … + p_m – 1) + l₂(q₁ + … + q_m – 1) и приравняем к нулю частные производные по всем аргументам: .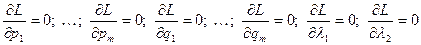

В результате получим следующую систему из (2m + 2)уравнений с (2m + 2) неизвестными:

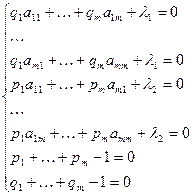
Решение этой системы и даёт смешанные стратегии для обоих игроков.

Нетрудно заметить, что исходная система уравнений включает две независимые подсистемы (для p_i, i =1, …, m, l₁ и q_j, j =1, …, m, l₂ соответственно), состоящие из (m + 1)уравнений с (m + 1)неизвестными, решение которых и даст искомые вероятности p_i и q_j, а также после подстановки этих вероятностей в формулу (3.1) цену игры V.

В качестве примера рассмотрим игру G(2´2), представленную в общем виде табл. 3.9.

Таблица 3.9

Bj Ai	B1	B2
A1	a11	a12
A2	a21	a22

V₁ = a₁₁p₁ + a₂₁p₂, V₂ = a₁₂p₁ + a₂₂p₂,

V = V₁q₁ + V₂q₂ = (a₁₁p₁ + a₂₁p₂)q₁ + (a₁₂p₁ + a₂₂p₂)q₂.

L = V + l₁(p₁ + p₂ – 1) + l₂(q₁ + q₂ – 1).

Приравняв к нулю частные производные функции Лагранжа по всем аргументам, получим следующую систему уравнений:

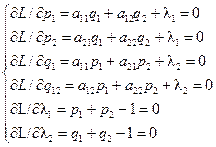
Решив данную систему получим следующие значения вероятностей:

.

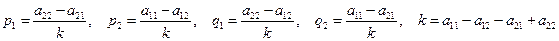Подставив полученные значения в выражение для V, получим цену игры.

Например, для игры G(2´2), представленной табл. 3.8, получим:

p₁=0,6; p₂=0,4; q₁=0,8; q₃=0,2; V =3,6.

Можно также найти решение в общем виде для игры G(3´3)и т.д.

Приведем более универсальный и достаточно легко компьютеризируемый способ решения матричных игр методом Лагранжа.

Рассмотрим игру игры G(3´3) в общем виде, представленную табл. 3.10.

Таблица 3.10

Bj Ai	B1	B2	B3
A1	a11	a12	a13
A2	a21	a22	a23
A3	a31	a32	a33

Для нахождения решения в смешанных стратегиях необходимо решить следующую систему уравнений:

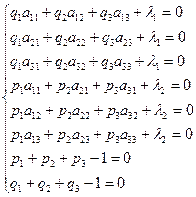
Эту систему можно представить следующим образом:

.

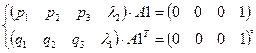
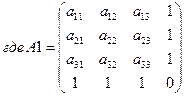Решением в общем виде представляется системой

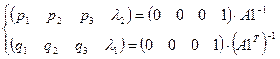
Более конкретно:

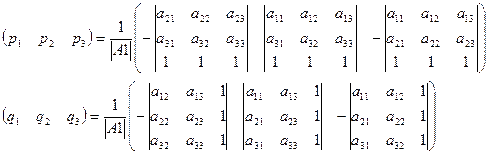
Обозначив

k = – a₁₁a₂₂ + a₁₁a₃₂ + a₁₁a₂₃ – a₁₁a₃₃ + a₂₁a₁₂ – a₂₁a₃₂ –

– a₂₁a₁₃ + a₂₁a₃₃ – a₃₁a₁₂ + a₃₁a₂₂ + a₃₁a₁₃ – a₃₁a₂₃ –

– a₁₂a₂₃ + a₁₂a₃₃ + a₂₂a₁₃ – a₂₂a₃₃ – a₃₂a₁₃ + a₃₂a₂₃,

получим итоговое решение:

p₁ = (– a₂₁a₃₂ + a₂₁a₃₃ + a₃₁a₂₂ – a₃₁a₂₃ – a₂₂a₃₃ + a₃₂a₂₃) / k

p₂ = ( a₁₁a₃₂ – a₁₁a₃₃ – a₃₁a₁₂ + a₃₁a₁₃ + a₁₂a₃₃ – a₃₂a₁₃) / k

p₃ = (– a₁₁a₂₂ + a₁₁a₂₃ + a₂₁a₁₂ – a₂₁a₁₃ – a₁₂a₂₃ + a₂₂a₁₃) / k

q₁ = (– a₁₂a₂₃ + a₁₂a₃₃ + a₂₂a₁₃ – a₂₂a₃₃ – a₃₂a₁₃ + a₃₂a₂₃) / k

q₂ = ( a₁₁a₂₃ – a₁₁a₃₃ – a₂₁a₁₃ + a₂₁a₃₃ + a₃₁a₁₃ – a₃₁a₂₃) / k

q₃ = (– a₁₁a₂₂ + a₁₁a₃₂ + a₂₁a₁₂ – a₂₁a₃₂ – a₃₁a₁₂ + a₃₁a₂₂) / k

V = – |A| / |A1|,

где А — исходная матрица игры.

Данный подход легко применим для произвольной игры G(m´m): строится матрица A1, далее, используя определители, записываются выражения для p_i и q_j, множитель знака для них будет равен (–1)^{m + i + 1}.