Метод a-b отсечений
Идея улучшения метода максимина за счет совмещения этапов построения дерева и отсечения неперспективных продолжений была предложено Дж. Маккарти (J. McCarthy) в 1961 г.
Существуют два вида a-b отсечения:
· неглубокое a-b отсечение;
· глубокое a-b отсечение.
Неглубокое a-b отсечение
Рассмотрим дерево игры на рис. 2.3.
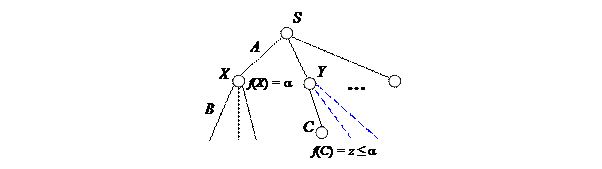 Рис. 2.3. Неглубокое a-b отсечение
Рис. 2.3. Неглубокое a-b отсечение
Пусть известны оценки f(X) = a и f(C) = z£a.. Справедлива следующая лемма.
Лемма 2.2. Если f(C) £ a, то ветви, исходящие из вершины Y и обозначенные штриховой линией, можно отсечь.
Доказательство. Так как игрок B стремится минимизировать оценочную функцию, то оценка вершины Y будет не больше z, т.е. f(Y) £ f(C) £ a. Следовательно, вершина Y не будетконкурировать с вершиной X при выборе игрока A, так как f(Y) £ f(X), что и означает неперспективность ветвей, исходящих из вершины Y.
Мы рассмотрели a отсечение, соответствующее выбору игрока A. Аналогичные рассуждения справедливы и для bотсечения в ситуации, когда выбор делает игрок B при справедливости следующих оценок: f(X)=b, f(C)= w ³ b.
Глубокое a-b отсечение
Рассмотрим дерево игры на рис. 2.4. Пусть известны оценки f(X) = a и f(E) = z £ a..
Докажем следующую лемму.
Лемма 2.3. Если f(E) £ a, то ветви, исходящие из вершины D и помеченные штриховой линией, можно отсечь.
Доказательство. Так как игрок B стремится минимизировать оценочную функцию, то для вершины D будет справедлива следующая оценка f(D) £ f(E) £ a, а для вершины C, ход из которой делает игрок A, стремящийся максимизировать оценочную функцию, соответственно f(C) ³ f(D).
Рассмотрим две возможности:
1. f(C) = f(D), что означает f(C)£ f(E)£a, т.е. имеем согласно лемме 2.2 неглубокое a отсечение, означающее неперспективность для игрока A вообще всех продолжений из вершины Y.
2. f(C) > f(D), что означает неучастие (неперспективность) вершины D для получения оценки f(C).
Лемма доказана.
Рис. 2.5 иллюстрирует применение метода a-bотсечений.
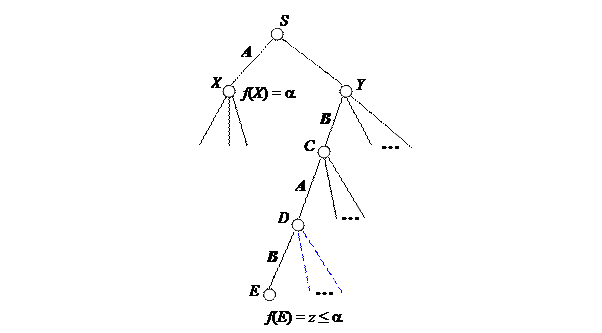
Рис. 2.4. Глубокое a-b отсечение
Из рис. 2.5 видно, что игроку A рекомендуется в качестве первого хода выбрать продолжение, ведущее к вершине X.
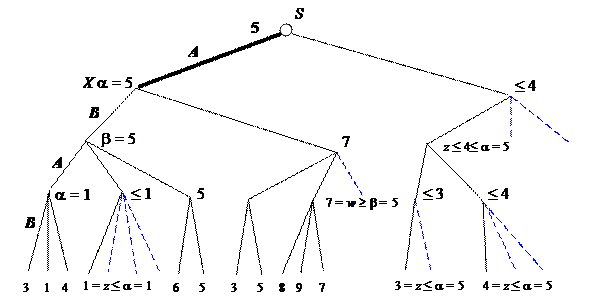
Рис. 2.5. Применение метода a-b отсечений
Табл. 2.1 иллюстрирует процедуру a-bотсечения.
Таблица 2.1
| Ход | Наилучшая оценка | Позиция на глубину | Оценка позиции | Условие отсечения | Действие |
| A (max) | a | Своя | z | z £ a | a отсечение |
| B (min) | b | Противника | w | w ³ b | b отсечение |
Заметим, что оценка a возрастает при движении по дереву снизу вверх, а оценка b,наоборот,убывает.
Приведем сравнительные оценки методов максимина и a-bотсечений. Пусть оценивается дерево на глубину ходов (уровней) n (для равенства ходов игроков n должно быть четным) и на каждом уровне имеется m вариантов выбора. Тогда сложность вычислений равна:
· mn для метода максимина;
· »2mn/2 для метода a-b отсечения.
Таким образом, метод a-b отсечений позволяет при тех же затратах памяти, что и метод максимина, построить дерево в среднем на глубину, в два раза большую, а значит, найти более качественное решение. Эффективность метод a-b отсечений возрастает, если удается предварительно упорядочить оцениваемые вершины по убыванию оценки a и возрастанию оценки b.
К недостаткам рассмотренных методов относятся:
· по сути оба метода не являются стратегиями и базируются на классических переборных алгоритмах с использованием оценочной функции;
· наличие эффекта горизонта, т.е. методы «не видят» выигрыша, который находится за горизонтом (ниже по дереву) оцениваемых вершин.
2.3. Контрольные вопросы к разделу 2
1. Перечислите возможные виды представления антагонистической игры.
2. Дайте определение класса информации.
3. Сформулируйте лемму 2.1.
4. Приведите пример представления антагонистической игры в виде дерева.
5. Назовите возможные методы поиска решений на дереве игры.
6. Дайте определения допустимого и оптимального алгоритмов поиска.
7. Поясните максиминный метод поиска решения.
8. Поясните неглубокое a-b отсечение.
9. Сформулируйте лемму 2.2.
10. Дайте доказательство леммы 2.2.
11. Поясните глубокое a-b отсечение.
12. Сформулируйте лемму 2.3.
13. Дайте доказательство леммы 2.3.
14. Приведите сравнительные оценки методов максимина и a-b отсечений.
15. Перечислите основные недостатки методов максимина и a-bотсечений.
Дата добавления: 2020-06-09; просмотров: 821;











