Представление антагонистической игры

Рассмотрим антагонистическую игру G(m´n),где у первого игрока A имеется множество стратегий {A_i}, i =1, …, m, а у второго игрока B – множество стратегий {B_j}, j =1, …, n.

Игра G(m´n)может быть представлена в виде дерева игры и в виде матрицы (матрицы платежей).

Представление игры в виде дерева является универсальным, т.е. любая игра может быть представлена в виде дерева, матричное представление не является универсальным – не любая игра может быть приведена к матричной форме.

Рассмотрим представление антагонистической игры G(m´n) в виде дерева.

Корневая вершина дерева представляет начальную ситуацию (состояние), промежуточные вершины – промежуточные ситуации, возможные в игре, концевые вершины – все возможные исходы игры, взвешенные платежами – выигрышами игрока A (соответственно, проигрышами игрока B). Дуги – представляют возможные переходы, возникающие в результате личных или случайных ходов, причем личные ходы выполняются игроками согласно выбранных ими стратегий.

Проиллюстрируем процесс построения дерева игры на следующем примере.

Имеется два игрока – A, B.

· 1 ход (личный): игрок А выбирает одну из двух цифр – 1 или 2;

· 2 ход (случайный): бросается монета и если выпадает «герб» (Г), то игроку В сообщается о выборе игрока А, если выпадает «решетка» (Р), то не сообщается;

· 3 ход (личный): игрок В выбирает одну из двух цифр – 3 или 4.

Платеж определяется следующим образом. Суммируются выборы игроков А и В, и если сумма чётная, то она выплачивается игроком В игроку А, если сумма нечетная, то игрок А платит игроку В. Соответствующее дерево игры представлено на рис. 2.1.

Определение 2.1. Классом информации S называется множество вершин дерева, в которых игроку, делающему личный ход, доступна одна и та же информация.

Для рассматриваемого примера имеется четыре класса информации (см. рис. 2.1): S₁, S₂ и S₄, содержащие по одной вершине, и S₃, который содержит две вершины.

Нетрудно доказать следующую лемму.

Лемма 2.1.Для игрыс неполной информацией имеется хотя бы один класс информации, содержащий две или более вершин. Соответственно для игры с полной информацией все классы информации содержат по одной вершине.

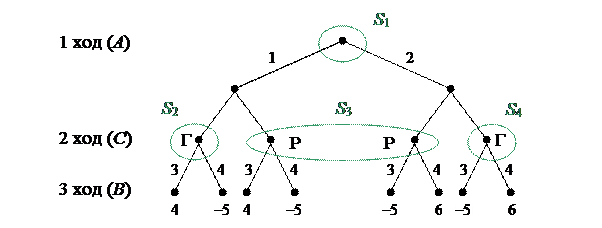
Рис. 2.1. Дерево игры

Так как класс S₃включает две вершины, то, следовательно, в общем случае имеем игру с неполной информацией. Отметим, что в частном случае, когда выпадает «герб» и игроку В сообщается о выборе игрока А, данная игра становится игрой с полной информацией.

Определим множества стратегий игроков.

Очевидно, что у игрока А имеется всего две стратегии (для класса информации S₁): A₁– выбор 1, A₂ – выбор 2.У игрока В стратегией B_i является правило (a, b,d), определяющее выбор игрока в классах информации S₂(a), S₃(b)и S₄(d).Следовательно, у игрока В имеется восемь стратегий: B₁=(3; 3; 3), B₂=(3; 3; 4), …, B₈=(4; 4; 4).