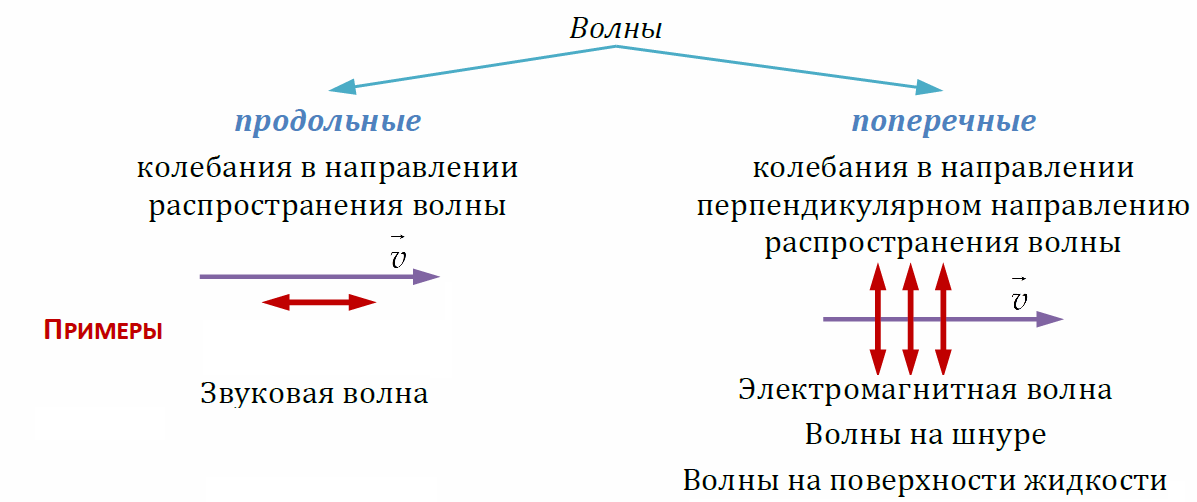
Продольные и поперечные волны. Уравнение бегущей волны. Уравнение плоской бегущей синусоидальной волны и его анализ.
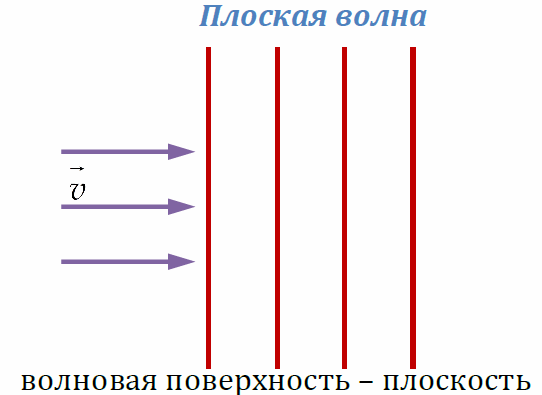
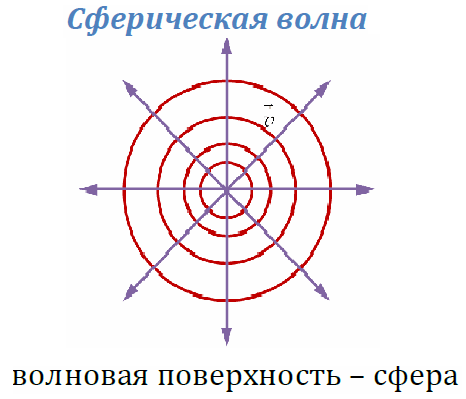
 Волновой фронт (волновая поверхность) – геометрическое место точек, в которых в один и тот же момент времени колебания происходят в одинаковой фазе. Часто встречающиеся примеры – плоский и сферический волновой фронт - показаны на РИС.
Волновой фронт (волновая поверхность) – геометрическое место точек, в которых в один и тот же момент времени колебания происходят в одинаковой фазе. Часто встречающиеся примеры – плоский и сферический волновой фронт - показаны на РИС.
Гармоническая (монохроматическая, синусоидальная) волна – процесс распространения гармонических колебаний в пространстве. Уравнение гармонических колебаний: 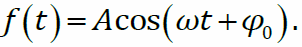
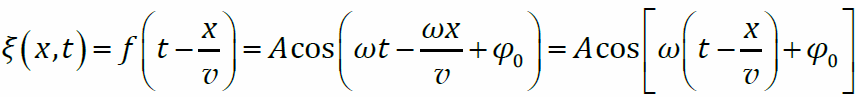
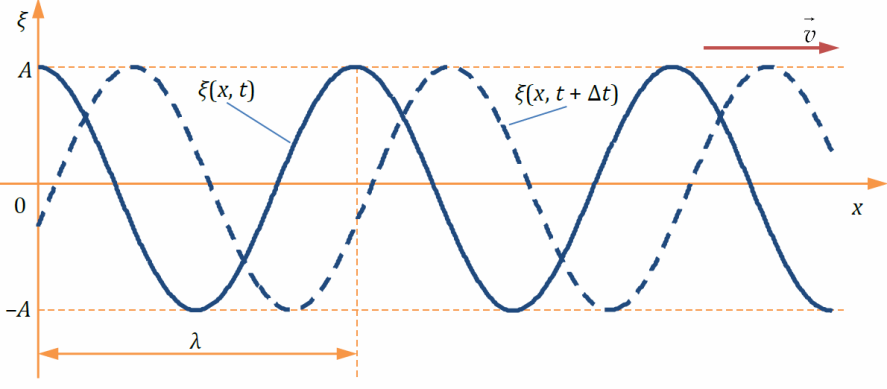
- Уравнение бегущей волны
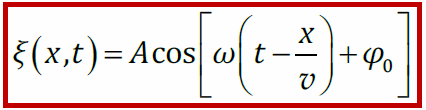 – уравнение плоской бегущей гармонической волны, где v – скорость,
– уравнение плоской бегущей гармонической волны, где v – скорость,
φ0 - начальная фаза, ω - циклическая частота,A – Амплитуда( максимальное значение колеблющейся величины)
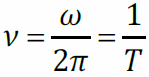
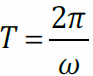
- период,- частота
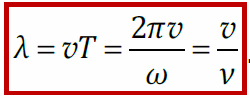 - Длина волны (расстояние, которое волна проходит за время одного полного колебания) - Длина волны (расстояние, которое волна проходит за время одного полного колебания)
| - Волновое число 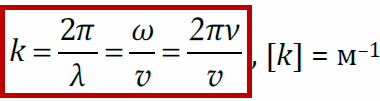
|
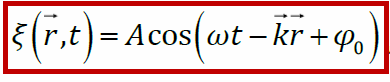
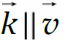 В общем случае (при произвольной форме волнового фронта) уравнение бегущей гармонической волны
В общем случае (при произвольной форме волнового фронта) уравнение бегущей гармонической волны
k – волновой вектор;
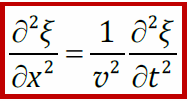
– волновое уравнение.
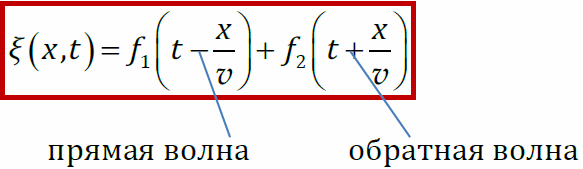
Общее решение волнового уравнения
Вид функцийf1 и f2 определяется начальными условиями.
Дата добавления: 2016-07-05; просмотров: 5476;











