Расчёт валов. Ведущий вал мультипликатора ТРКП
Расчёт валов проводится с целью определения геометрических параметров (диаметров), способных выдерживать требуемые нагрузки, а также для проверки прочности спроектированного вала при действии знакопеременных нагрузок в условиях циклической усталости.
 Проследим порядок расчёт вала на примере вала первой ступени цилиндрического мультипликатора ТРКП (рис. 5.1) пассажирского вагона [31, 53], ременную передачу которого мы рассчитывали выше.
Проследим порядок расчёт вала на примере вала первой ступени цилиндрического мультипликатора ТРКП (рис. 5.1) пассажирского вагона [31, 53], ременную передачу которого мы рассчитывали выше.
Ведущий вал цилиндрического одноступенчатого мультипликатора получает вращение от ведомого шкива клиноременной передачи.
На ведущем вале должно быть установлено зубчатое колесо, передающее вращающий момент ведомому валу, откуда он передаётся на электрогенератор.
Расчёты валов проводятся в три этапа.
Предварительный расчёт вала производится после того, как станут известны вращающие моменты на всех ступенях проектируемого передаточного механизма. Из энергокинематического расчёта провода ТРКП известен вращающий момент на ведомом шкиве М2 = 105 Нм. Пока форма вала ещё не разработана, вал на этой стадии представляется гладким цилиндрическим стержнем. Предполагается использовать сталь 40Х, применяемую для большинства валов.
В результате предварительного расчёта вычисляется минимальный диаметр каждого вала. Предварительно примем заниженное допускаемое напряжение кручения [t ]кр = 35 МПа, тогда:
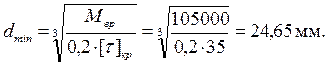
Вычисленный предварительный минимальный диаметр округляется до ближайшего большего из нормального ряда (таб. 5.1):
Принимаем dmin = 25 мм. Этот минимальный диаметр вала используется при рисовании эскизной компоновки редуктора.
| Таблица 5.1 Нормальные ряды диаметров валов, мм | |
| Предпочтительный | 10; 12; 14; 16; 18; 20; 22; 25; 28; 32; 36; 40; 45; 50; 55; 60; 70; 80; 90; 100; 110; 125 |
| Дополнительный | 10,5; 11; 11,5; 13; 15; 17; 19; 21; 24; 28; 30; 33; 35; 38; 42; 48; 52; 53; 63; 65; 75; 85; 95; 105; 120; 125; 130 и через 10 мм. |
Уточнённый расчёт валов производится после предварительного расчёта валов и расчёта передач и выполнения эскизной компоновки, когда известны длины валов, нагрузки, места размещения деталей передач, опор (подшипников) и расстояния между ними. Расчёт ведётся в следующем порядке.
Строим расчётную схему вала в виде:
− балки с заделкой, если он установлен в длинных (l > d) подшипниках скольжения или в подшипниках качения по два и более несамоустанавливающихся подшипника в опоре;
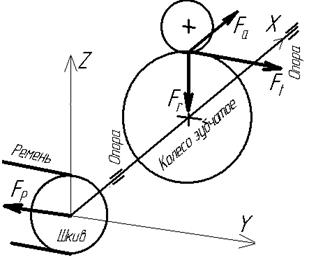
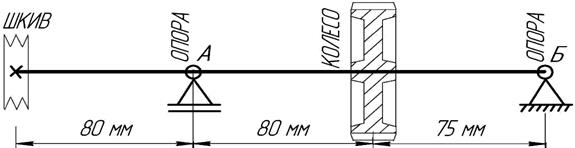
− балки на шарнирных опорах, если он установлен в коротких подшипниках скольжения (l << d) или в подшипниках качения (по одному или по два самоустанавливающихся в каждой опоре). При этом реакции опор прикладываются в середине длины подшипника. Это как раз соответствует нашему случаю (рис. 5.2…3).
|
| Рис. 5.2. Схема вала и действующих сил |
−
|
| Рис. 5.3. Расчётная схема вала |
Поскольку линии действия сил расположены в разных плоскостях, то выбираем две взаимно-перпендикулярные плоскости (обычно горизонтальная XOY и фронтальная YOZ) и расчетные схемы рассматриваем в каждой из этих плоскостей, на которые проектируем все действующие на вал силы (рис. 5.4).
Вычисляем реакции опор и строим эпюры изгибающих моментов в каждой плоскости.

Рассчитываем суммарные изгибающие моменты и строим их эпюры для каждой точки перелома MΣИЗГ = (MZИЗГ2 + MYИЗГ2)1/2 (рис. 5.5).

Строим эпюру вращающего момента MВР (М2) (рис. 5.6)

Вычисляем эквивалентные моменты (рис. 5.7) для всех переломных точек эпюр MΣИЗГ и MВР: МЭКВ=(МΣИЗГ2 + a МВР2)1/2, где a= 0,75 или a=1 в зависимости от принятой теории прочности. Принимаем a=1.

Определяем уточненный диаметр вала по эквивалентным моментам для каждого характерного сечения (под подшипниками, под колесами, в сечениях с наибольшим МЭКВ) и округляем его до ближайшего большего по нормальному ряду (табл. 5.1).
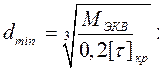
− в сечении под ременным шкивом: dmin = (105000/0,2·35)0,33 = 24,65 ≈ 25 мм;
− в сечении А под опорой: dmin = (114795/0,2·35)0,33 = 25,39 ≈ 28 мм;
− в сечении под зубчатым колесом: dmin = (165792/0,2·35)0,33 = 28,71≈ 32 мм.
Форма проектируемого вала может стать очень сложной, ступенчатой, но нигде диаметр вала не может быть меньше рассчитанного минимального.
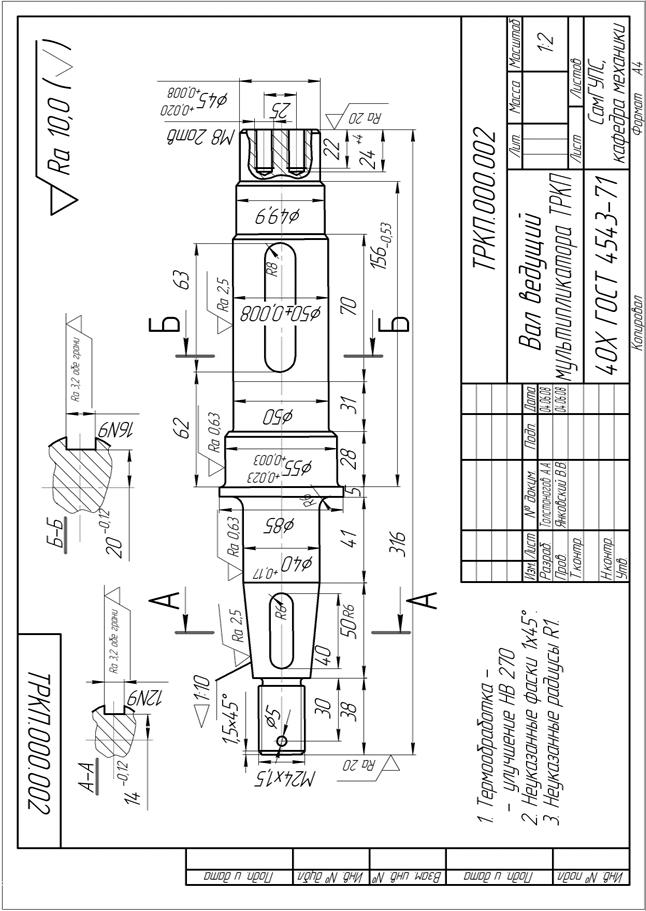
Проверочный расчёт валов выполняется, когда уже выполнен рабочий чертёж вала (рис. 5.8), т.е. известны диаметры всех участков, радиусы сопряжений, размеры пазов и канавок, шлицы, отверстия, выточки и т.п.
В качестве критерия прочности здесь выступает коэффициент запаса прочности для опасного сечения [1, 8, 12, 34], поскольку поломки валов носят усталостный характер вследствие циклического характера напряжений. Этот расчёт выполняют, как проверочный, т.е. вычисляется коэффициент запаса прочности и сравнивается с требуемым
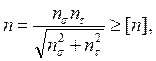
где [n] – требуемый коэффициент запаса прочности [n] = 1,3…1,5 для обеспечения только прочности, [n] = 2,4…4 для обеспечения и прочности и жёсткости;
|
| Рис. 5.8. Рабочий чертёж вала |
ns и nt – коэффициенты запаса прочности по нормальным и касательным напряжениям
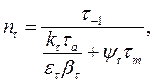
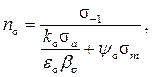
где s–1 и τ–1 – пределы выносливости материала вала при изгибе и кручении с симметричным циклом, их находят по известному пределу прочности материала: для углеродистых сталей s–1 » 0,43sВ; для стали 40Х sВ = 850 МПа, а s–1 » 0,43·850 » 365 МПа; для легированных сталей s–1 » 0,35 sВ + (70 … 120) Н/мм2;предел выносливости при кручении τ–1 = (0,5…0,58)s–1; для 40Х τ–1 » 0,56·850 » 476 МПа;
sa и τa – амплитудные значения напряжений sa = MΣИЗГ/W ; τa=MВР/2Wк;
sm и τm – средние напряжения цикла (sm=0, τm=τa);
εσ и ετ – масштабные коэффициенты диаметра вала, зависящие от вида нагружения и диаметра вала (табл. 5.2):
| Таблица 5.2 Значения масштабного коэффициента εσ или ετ | |||||||
| Вид нагружения и материал | Диаметр вала, мм | ||||||
| Изгиб для углеродистой стали | 0,92 | 0,88 | 0,85 | 0,81 | 0,76 | 0,70 | 0,61 |
| Изгиб для легированной стали и кручение для всех сталей | 0,83 | 0,77 | 0,73 | 0,70 | 0,65 | 0,59 | 0,52 |
− для участка вала d = 50 мм со шпоночным пазом принимаем εσ= 0,81; ετ= 0,70;
− для участка вала d = 40 мм с галтелью принимаем εσ= 0,85; ετ= 0,73;
ψσ и ψτ – коэффициенты влияния среднего напряжения цикла на усталостную прочность, зависят от типа стали (табл. 5.3):
| Таблица 5.3 Коэффициенты влияния среднего напряжения ψσ и ψτ | ||
| Стали | Коэффициенты | |
| ψσ | ψτ | |
| Углеродистые мягкие | 0,15 | 0,05 |
| Среднеуглеродистые | 0,20 | 0,10 |
| Легированные | 0,25 | 0,15 |
для среднеуглеродистой стали 40Х примем ψσ= 0,20; ψτ= 0,10;
βσ и βτ – коэффициенты, учитывающие шероховатость поверхности (табл. 5.4):
| Таблица 5.4 Коэффициенты βσ и βτ, учитывающие шероховатость поверхности | |||||
| Механическая обработка | Шероховатость Rа, мкм | βσ при σВ, МПа | βτ при σВ, МПа | ||
| ≤ 700 | > 700 | ≤ 700 | > 700 | ||
| Шлифование тонкое | до 0,2 | ||||
| Обтачивание тонкое | 0,2…0,8 | 0,99..0,93 | 0,99..0,91 | 0,99..0,96 | 0,99..0,95 |
| Шлифование чистовое | 0,8…1,6 | 0,93..0,89 | 0,9..0,86 | 0,96..0,94 | 0,95..0,92 |
| Обтачивание чистовое | 1,6…3,2 | 0,89..0,86 | 0,86..0,82 | 0,94..0,92 | 0,92..0,89 |
− для участка вала d = 50 мм со шпоночным пазом после чистового обтачивания на Rа2,5 примем βσ = 0,82; βτ = 0,89;
− для шейки с галтелью после тонкого обтачивания на Rа0,125 примем βσ= 0,91; βτ= 0,95.
kσ и kτ – коэффициенты концентрации напряжений при изгибе и кручении, учитывающие галтели, шпоночные канавки, прессовые посадки и резьбу, определяются из таблицы (табл. 5.2);
| Таблица 5.2 Коэффициенты концентрации напряжений kσ и kτ | |||||||
| Концентратор | kσ | kτ | Эскиз | Моменты сопротивления | |||
| sв, Н/мм2 | W, мм3 | WK, мм3 | |||||
| £ 700 | ³1000 | £ 700 | ³1000 | ||||
| r /d = 0,02 Галтель 0,06 (D/d = 1,25..2) 0,10 | 2,50 1,85 1,60 | 3,50 2,00 1,64 | 1,80 1,40 1,25 | 2,10 1,53 1,35 | 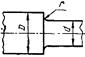
| 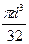
| 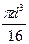
|
| Поперечное отверстие a/d =0,05 …0,25 | 1,90 | 2,00 | 1,75 | 2,00 | 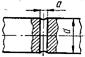
| 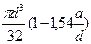
| 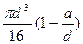
|
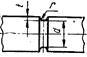
| r/d = 0,02 Выточка (t = r) 0,06 0,10 | 1,50 1,80 1,70 | 2,35 2,00 1,85 | 1,40 1,35 1,25 | 1,70 1,65 1,30 |
| 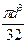
| 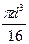
|
| Шпоночная канавка | 1,75 | 2,00 | 1,50 | 1,90 | 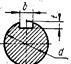
| 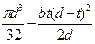
| 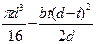
|
| Шлицы прямобочные x =1,25лёгкой серии x =1,205 средн. серии x = 1,265 лёгкой серии | 1,60 | 1,75 | 2,45 | 2,80 | 
| 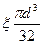
| 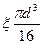
|
| Шлицы эвольвентные и валы-шестерни | 1,60 | 1,75 | 1,50 | 1,60 | 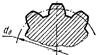
| 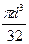
| 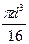
|
| Витки червяка | 2,30 | 2,50 | 1,70 | 1,90 | 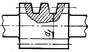
| 
| 
|
| Резьба | 1,8 | 2,4 | 1,2 | 1,5 | 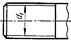
| 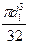
| 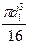
|
| Прессовая посадка | 2,4 | 3,6 | 1,8 | 2,5 | |||
| Примечание. При наличии нескольких концентраторов напряжений в одном сечении в расчёт принимается тот, у которого коэффициент концентрации наибольший. |
− для шпоночного паза глубиной t = 5 мм и шириной b = 16 мм, под зубчатым колесом d = 50 мм и MИЗГ = 33565 Нмм примем: W = πd3/32 − bt(d−t)2/2d =
= 10646 мм3, sa = MИЗГ/W =33565/10646 = 3,15 МПа; MВР = 105000 Нмм,
Wк= πd3/16 − bt(d−t)2/2d = 22911 мм3, τa= MВР/2Wк=105000/2·22911 = 2,29 МПа. По таблице 5.2 находим kσ = 1,875; kτ = 1,70;
− для галтели r6 на диаметре d = 40 мм и MИЗГ = 46400 Нмм примем: W = πd3/32 = 3,14·403/32 = 6280 мм3, sa = MИЗГ/W = 46400/6280 = 7,4 МПа; MВР = 105000 Нмм, Wк= πd3/16 = 3,14·403/16 = 12560 мм3, τa= MВР/2Wк =
= 105000/12560 = 8,5 МПа. Для r/d =0,15 по таб. 5.2 примем kσ = 1,62; kτ = 1,30;
По полученным данным вычисляем коэффициенты запаса:
− для участка вала d = 50 мм со шпоночным пазом:
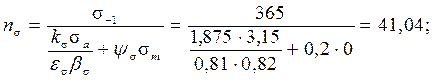
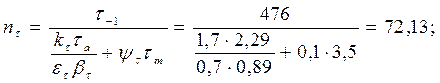
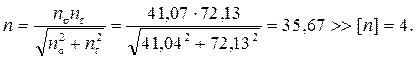
− для шейки с галтелью:
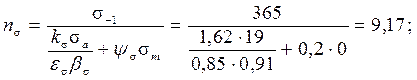
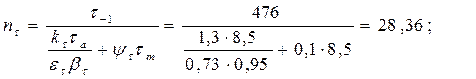
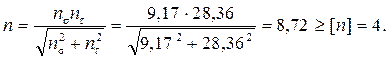
Видим, что для обоих опасных сечений коэффициенты запаса значительно больше, чем требуемые ([n] = 4) для обеспечения и прочности и жёсткости.
Аналогичным образом могут быть проверены опасные сечения валов с любыми конструктивными элементами.
Если коэффициент запаса оказывается меньше требуемого, то сопротивление усталости можно существенно повысить, применив поверхностное упрочнение: азотирование, поверхностную закалку токами высокой частоты, дробеструйный наклёп, обкатку роликами и т.д. При этом можно получить увеличение предела выносливости до 50 % и более.
Контрольные вопросы
С какой целью проводится расчёт валов?
На каком этапе проектирования проводится предварительный расчёт валов?
Как выполняется расчёт вала, если он нагружен силами, расположенными в разных плоскостях?
На каком этапе проектирования выполняется уточнённый расчёт валов?
На каком этапе и с какой целью выполняется проверочный расчёт валов?
Как в расчёте учитываются коэффициенты концентрации напряжений?
Какими мерами можно повысить сопротивление валов усталости?
Дата добавления: 2020-06-09; просмотров: 658;











