Проверяем цепь по допускаемой частоте вращения
n1max = 14 Z11/4 ·103/p = 14 · 20 1/4 · 103 / 25,4 = 1165 об/мин.
Таким образом, частота вращения (n1 = 111 об/мин) находится в допустимых пределах.
Задаём оптимальное межосевое расстояние А = 40р = 40·25,4 = 1016 мм.
Рассчитываем требуемое число звеньев:
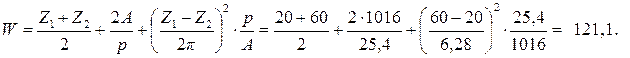 Принимаем чётное число звеньев цепи W = 120, чтобы не применять соединительного звена. Также, чётное число зубьев малой звёздочки (Z1 = 20) в сочетании с чётным числом звеньев цепи способствует уменьшению износа.
Принимаем чётное число звеньев цепи W = 120, чтобы не применять соединительного звена. Также, чётное число зубьев малой звёздочки (Z1 = 20) в сочетании с чётным числом звеньев цепи способствует уменьшению износа.
Уточняем межосевое расстояние по выбранному числу звеньев цепи:
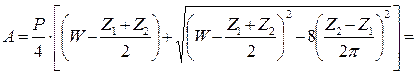
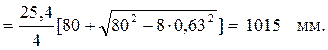
Во избежание повышенной нагрузки от силы тяжести и радиального биения звёздочек межосевое расстояние рекомендуют уменьшать на Δ = (0,002… 0,004)А. Уменьшим межосевое расстояние на Δ = 0,003А = 3,047 мм. Тогда
Аср = А – Δ = 1015,87 – 3,047 = 1012,82 ≈ 1010 мм.
Вычисляем натяжение от центробежных сил Fц = q·V2 = 2,6·0,942 = 2,3 H.
Коэффициент провисания цепи Kf зависит от угла наклона к горизонту β. Для горизонтальной цепи (β = 0°) Kf = 6, для вертикальной (β = 90°) Kf = 1.
В нашем случае β = 45° и мы принимаем Kf = 3.
Усилие от провисания цепи Fпров = g·Kf ·q· aср = 9,81· 3 ·2,6· 1010 = 77 H.
Находим величину допускаемого коэффициента запаса прочности [S]. Для шага цепи р = 25,4 мм и частоты вращения ведущей звёздочки n1 = 111 об/мин, допускаемый коэффициент запаса примем [S] = 7,8 (табл. 4.20).
Находим расчётный коэффициент запаса прочностиS
S = Fраз / (Ft · K1 + Fц + Fпров) = 60000/(1595 · 1,5 + 2,3 + 77) = 24,27.
Расчётный коэффициент запаса больше требуемого, условия прочности цепи выполняется.
Рассчитывается количество ударов цепи (проверка на долговечность)
 νц = 4 · Z1 · n1 / (60· W) = 4 · 20 · 111 / (60 · 120) = 1,23 c−1.
νц = 4 · Z1 · n1 / (60· W) = 4 · 20 · 111 / (60 · 120) = 1,23 c−1.
Полученное число ударов цепи при набегании на зубья звёздочек и сбегании с них сравнивается с допускаемым (таб. 4.21).
Для цепи ПР-25,4-60 допускаемое число ударов [νц] = 20 c−1. Принятая цепь проходит по критерию долговечности.
| Таблица 4.20 Допускаемый коэффициент [S] запаса прочности цепей | ||||||||||||||
| Шаг, р, мм | Частота вращения меньшей звёздочки n1, об/мин | |||||||||||||
| Значения [S] для роликовых цепей | ||||||||||||||
| 12,7 | 7,1 | 7,3 | 7,6 | 7,9 | 8,2 | 8,5 | 8,8 | 9,4 | 10,6 | 12,2 | 13,8 | 15,4 | ||
| 15,875 | 7,2 | 7,4 | 7,8 | 8,2 | 8,6 | 8,9 | 9,3 | 10,1 | 10,8 | 11,7 | 13,2 | 14,8 | 16,3 | |
| 19,05 | 7,2 | 7,6 | 8,0 | 8,4 | 8,9 | 9,4 | 9,7 | 10,8 | 11,7 | 12,9 | 16,3 | – | – | |
| 25,4 | 7,3 | 7,6 | 8,3 | 8,9 | 9,5 | 10,2 | 10,8 | 12,0 | 13,3 | 14,0 | 16,3 | – | – | – |
| 31,75 | 7,4 | 7,8 | 8,6 | 9,4 | 10,2 | 11,0 | 11,8 | 13,4 | 14,8 | 16,3 | 19,5 | – | – | – |
| 38,1 | 7,5 | 8,0 | 8,9 | 9,8 | 10,8 | 11,8 | 13,4 | 14,8 | 16,3 | 19,5 | – | – | – | – |
| 44,45 | 7,6 | 8,1 | 9,2 | 10,3 | 11,4 | 12,5 | 14,0 | 16,3 | – | – | – | – | – | – |
| 50,8 | 7,6 | 8,3 | 9,5 | 10,8 | 12,0 | 13,6 | – | – | – | – | – | – | – | – |
-
| Таблица 4.21 Допускаемое число ударов[ν]в секунду | |||||||
| Тип цепи | Шаг цепи р, мм | ||||||
| 12,7 | 15,875 | 19,05 | 25,4 | 31,75 | 38,1 | 44,45 | |
| Роликовая | |||||||
| Зубчатая | – | – |
Находим нагрузку от цепи на вал Fв = Ft + 2Fпров = 1595 + 2·77 = 1749 H.
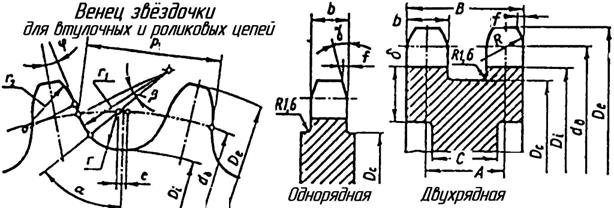
Определяем геометрические параметры звёздочек (рис. 4.18):
– диаметры делительных окружностей:
dW1 = P/sin(180°/Z1) = 25,4/sin(180°/20) = 162,4 мм;
dW2 = P/sin(180°/Z2) = 25,4/sin(180°/60) = 485,7 мм.
|
| Рис. 4.18. Конструкции звёздочек цепной передачи |
– коэффициент высоты зуба k зависит от соотношения шага цепи и диаметра ролика (P/d1), в нашем случае P/d1 = 25,4/15,88 = 1,59. Тогда k = 0,532.
| P/d1 = | 1,4…1,5; | 1,5…1,6; | 1,6…1,7; | 1,7…1,8; | 1,8…2,00; |
| k= | 0,480; | 0,532; | 0,555; | 0,575; | 0,565; |
– диаметры окружностей выступов:
de1 = P[k+ctg(180°/Z1)] = 25,4[0,532+ctg(180°/20)] = 171,05мм;
de2 = P[k+ctg(180°/Z2)] = 25,4[0,532+ ctg(180°/60)] = 510,11 мм;
– радиус впадин r = 0,5025d1 + 0,05= 0,5025∙15,88 + 0,05 = 8,03 мм;
– диаметры окружностей впадин:
di1 = dW1 − r = 162,4 – 8,03 = 154,4 мм;
di2 = dW2 − r = 485,7 – 8,03 = 477,0 мм;
– ширина зубчатого венца звёздочки b= 0,9Bвн – 0,15, где Bвн – расстояние между внутренними пластинами цепи, тогда b= 0,9∙15,88–0,15 = 14,14 мм;
– радиус кривизны r2 и координату h центра кривизны головки зуба для плавного набегания цепи принимают: r3 = 1,7 · d1 = 1,7 · 15,88 = 26,99 мм;
h = 0,8 · d1= 0,8 · 15,88 = 12,70 мм;
– диаметр вала 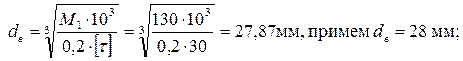
проверяем конструктивное соотношение dW1/dв = 162,4/28 = 5,8; если соотношение диаметров окажется больше 10, то пересчитывают диаметр вала так, чтобы было dв = d1 / 10;
– диаметр ступицы dст = (1,6 …2,0)dв = 45…56; принимаем dст = 50;
– длина ступицы lст= (1,6 …1,8)dв = 45…50,4. Примем lст= 50;
– диаметр обода (наибольший):
D01 = p·ctg(180°/Z1) − 1,3b = 25,4·ctg(180°/20) − 1,3 · 14,14 = 141,90 мм;
D02 = p·ctg(180°/Z2) − 1,3b = 25,4·ctg(180°/60) − 1,3 · 14,14 = 466,25 мм.
По результатам расчётов окончательно назначаем для заданного привода цепь ПР-25,4-60 ГОСТ 13568-97, c рассчитанными геометрическими параметрами и отвечающую требованиям:
износостойкости p = 23,9 МПа < [p] = 32 МПа;
прочности S = 35,4 > [S] = 24,27;
долговечности νц = 1,23 с–1 < 20 с–1.
По рассчитанным параметрам выполняется рабочий чертёж звёздочки (рис. 4.19).
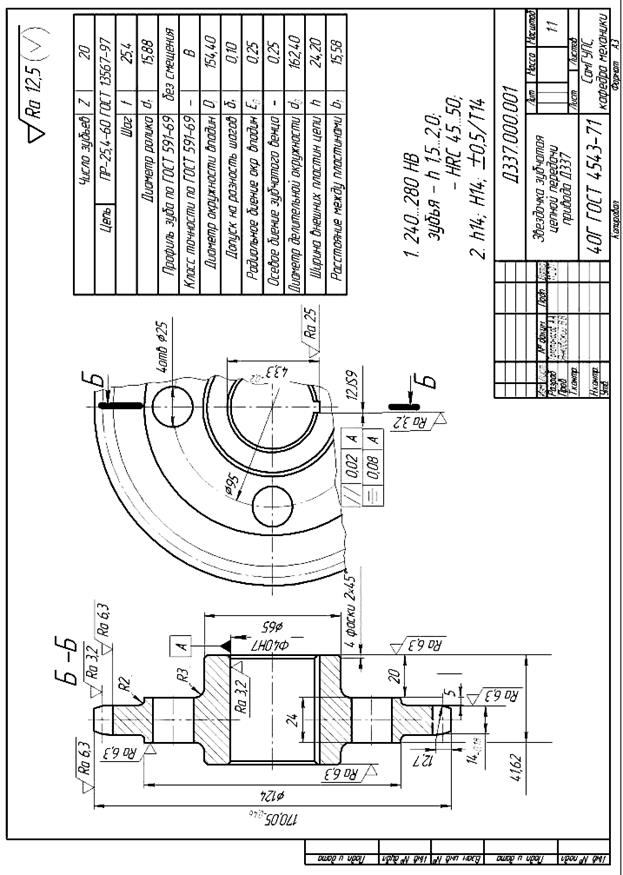
|
| Рис. 4.19. Рабочий чертёж звёздочки цепной передачи |
Контрольные вопросы
В каких конструкциях могут применяться фрикционные передачи?
Когда применяются фрикционные передачи с постоянным передаточным отношением?
В каких случаях могут применяться неметаллические фрикционные передачи?
В каком скоростном диапазоне обычно применяются ременные передачи?
Что является исходными данными для расчёта ременных передач?
Какова цель проектного и проверочного расчётов ременных передач?
В чём особенности применения плоскоременных и клиноременных передач?
Что является исходными данными для расчёта ременных передач?
Какие параметры ремней и ременных передач стандартизованы в нормальных рядах?
Как выбирается сечение клиновых ремней при расчёте передачи?
В чём особенности расчёта и выбора поликлиновых ремней?
По каким критериям находят минимальный диаметр шкива передачи?
Из чего складываются суммарные напряжения в ремне?
Каковы особенности конструкции и применения зубчатоременных передач?
Какие меры компенсируют высокую чувствительность зубчатоременных передач к неточностям монтажа?
Какие натяжные устройства применяют для ременных передач?
Каковы обязательные монтажные требования к ременным передачам?
Как различают цепи по характеру работы цепных передач?
Какие коэффициенты учитывают в расчёте условия эксплуатации цепи?
Какую роль в расчёте цепи играет удельное контактное давление?
Дата добавления: 2020-06-09; просмотров: 646;











