Синтез алгоритма управления на примере системы третьего порядка.
Рассмотрим синтез алгоритма управления на примере системы третьего порядка. Обобщение алгоритма на системы более высокого порядка не представляет сложности.
Пусть дифференциальное уравнение объекта имеет вид
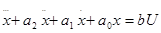 (116)
(116)
где 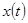 - скаляр - выходная переменная; U-управление.
- скаляр - выходная переменная; U-управление.
На вход системы поступает сигнал 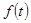 ,который должен воспроизводиться переменной
,который должен воспроизводиться переменной 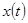 . Поставим задачу формирования управления
. Поставим задачу формирования управления
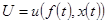
минимизирующего ошибку системы.
Введем интервал квантования T и будем стремиться к тому, чтобы в моменты времени t=kT,k=0,1,… выходной сигнал и его первая производная совпадали с входным сигналом и его первой производной. При этом управление строится отдельно на каждом временном отрезке 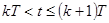 . Пусть при t=kT известны величины x[kT],f[kT]. Предположим далее, что можно измерить или вычислить производную
. Пусть при t=kT известны величины x[kT],f[kT]. Предположим далее, что можно измерить или вычислить производную 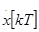 , а также , что в момент t=kT возможно экстраполировать функцию f(t) и оценить ее значение и значение ее первой производной при
, а также , что в момент t=kT возможно экстраполировать функцию f(t) и оценить ее значение и значение ее первой производной при 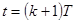 . Обозначим эти оценки
. Обозначим эти оценки 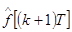 и
и 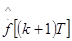 . Поставим задачу определения управления U(t) на отрезке
. Поставим задачу определения управления U(t) на отрезке 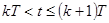 , переводящего изображающую точку на плоскости
, переводящего изображающую точку на плоскости 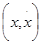 из начального положения
из начального положения 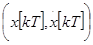 , в конечное положение (
, в конечное положение ( 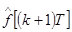 ,
, 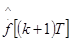 ) .
) .
Задачу определения управления будем решать как обратную задачу динамики , т.е. задавшись траекторией на плоскости 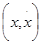 соединяющей имеющуюся начальную и желаемую конечную точки, найдем управление U при
соединяющей имеющуюся начальную и желаемую конечную точки, найдем управление U при 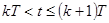 . Зададимся следующим законом изменения координаты x(t) :
. Зададимся следующим законом изменения координаты x(t) :
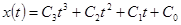 , (117)
, (117)
где время t отсчитывается заново для каждого отрезка. Коэффициенты 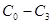 постоянны на каждом временном отрезке и изменяются при его смене.
постоянны на каждом временном отрезке и изменяются при его смене.
Определим коэффициенты 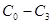 , исходя из начальных величин
, исходя из начальных величин 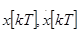 и желаемых конечных величин
и желаемых конечных величин 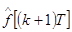 ,
, 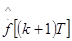 . Найдем производную
. Найдем производную 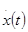 согласно формуле (117):
согласно формуле (117):
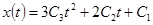 . (118)
. (118)
Тогда система уравнений для определения коэффициентов 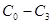 примет вид
примет вид
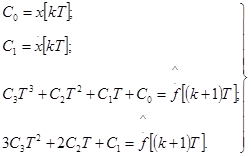 (119)
(119)
Система (119) всегда имеет единственное решение
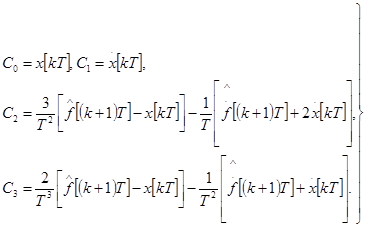 (120)
(120)
Найдем высшие производные по t выражения (117):
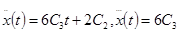 . (121)
. (121)
Подставляя выражения (117),(118),(121) с коэффициентами (120) в уравнение объекта (116), найдем
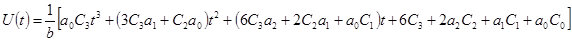 .
.
Здесь управление выражается в явном виде, так как уравнение (116) не содержит производных u(t) .
Данный алгоритм может быть реализован при использовании ЭВМ в контуре управления. При этом U(t) может реализовываться либо с помощью аналогового устройства с переменными коэффициентами, либо с помощью цифрового вычислительного устройства, работающего с периодом дискретности 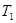 , значительно меньшим Т. Оценки
, значительно меньшим Т. Оценки 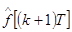 ,
, 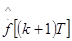 в простейшем случае могут получаться с помощью конечных разностей решетчатой функции
в простейшем случае могут получаться с помощью конечных разностей решетчатой функции 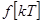 . Следует отметить, что даже при идеальной экстраполяции система будет следить за входным сигналом с ошибкой. Это объясняется тем, что в системе третьего порядка для однозначного задания движения необходимо знать еще и начальную величину ускорения
. Следует отметить, что даже при идеальной экстраполяции система будет следить за входным сигналом с ошибкой. Это объясняется тем, что в системе третьего порядка для однозначного задания движения необходимо знать еще и начальную величину ускорения 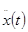 . Здесь же контролируются только координата и ее первая производная. Процесс (117) возможен при условии
. Здесь же контролируются только координата и ее первая производная. Процесс (117) возможен при условии
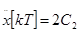 .
.
В противном случае реальный процесс x(t) отличается от определяемого по формуле (117) и в точку ( 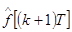 ,
, 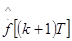 ) система попадет с некоторой сшибкой, к которой еще добавится ошибка экстраполяции. Однако приведенный алгоритм не накапливает ошибки, более того, возникшую на каком-либо этапе ошибку он постарается исправить на следующем шаге. При необходимости можно включить в число контролируемых параметров и вторую производную
) система попадет с некоторой сшибкой, к которой еще добавится ошибка экстраполяции. Однако приведенный алгоритм не накапливает ошибки, более того, возникшую на каком-либо этапе ошибку он постарается исправить на следующем шаге. При необходимости можно включить в число контролируемых параметров и вторую производную 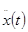 .
.
Дата добавления: 2016-07-05; просмотров: 1508;











