Синтез ЦСУ с апериодическим переходным процессом.

План лекции:

1. Общие положения.

2. Пример решения задач синтеза ЦСУ с минимальным временем ПП.

3. Общий случай синтеза системы с апериодическим переходным процессом.

Общие положения.

Рассмотренные способы синтеза базировались на основе непрерывных систем, использующих ЛАФЧХ, регуляторы с опережением или отставанием по фазе. Однако структура ЦР отличается большой гибкостью, поэтому можно разработать оригинальные методы, отличные от метода синтеза непрерывных САУ.

Большая часть СУ проектируется так, чтобы переходный процесс в них возможно быстрее достигал требуемого значения. Этот класс систем называется системами с минимальным временем переходных процессов или системами оптимальными по быстродействию. Решение задач синтеза ЦСУ с минимальным временем ПП рассматривается далее.

Пример.

Рассмотрим пример:

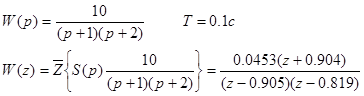
Пусть последовательный цифровой регулятор имеет ПФ

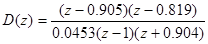
Тогда ПФ разомкнутой скорректированой системы

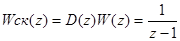
То есть введение КУ приводит к компенсации всех нулей и полюсов исходной системы и появлению нового полюса Z=1

Соответствующая ПФ замкнутой системы:

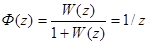
Тогда при ступенчатом входном сигнале

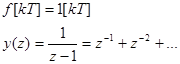
Это означает, что выходной сигнал у[kT] достигает требуемого значения за один период квантования и с этого момента сохраняет требуемое значение. Перерегулирование нулевое. Однако в общем случае, хотя у(кТ) может иметь малое перерегулирование, действительная реакция у(t) может сопровождаться импульсами.

Так как Т<< постоянных времени объекта, можно ожидать, что y[kT] достаточно хорошо совпадает с y(t). Поэтому можно ожидать, что переходная функция достигает установившегося значения через Т=0.1с, а между моментами квантования пульсаций не будет или они будут малы. Такой тип реакции называется апереиодическим переходным процессом.

Апериодический переходный процесс можно получить только в случае, когда есть полная компенсация нулей и полюсов. На практике реальное ограничение приводит к тому, что достичь идеального апериодического процесса невозможно.

3. Общий случай синтеза системы с апериодическим переходным процессом.

Рис. 54.

Что должно быть в результате синтеза:

1. Нулевая установившаяся ошибка при определении входного сигнала.

2. Длительность переходного процесса должна быть минимальной

3. Цифровой регулятор должен быть физически реализуемым

ПФ замкнутой скорректированной системы имеет вид:

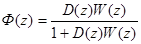(1)

откуда

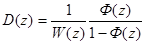(2)

при этом

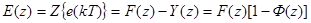(3)

Будем рассматривать класс входных сигналов, изображение которых имеет вид:

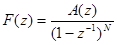(4)

где N-натуральное число

A(z)- многочлен от z

В общем случае выражение (*) соответствует входному сигналу типа

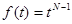
Например, при

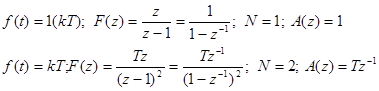
С учетом (*), используя теорему определьном значении найдем установившуюся ошибку

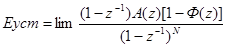(5)

Исходя из полученного выражения выясним, что необходимо, чтобы Еуст=0. Так как А(1)<>0,то очевидно, что для этого 1-Ф(z) должно содержать скобку 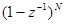т.е.

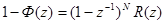(6)

где R(z)-полином от Z

Следствием того, что 1-Ф(z) представимо в форме (6) будет выражение:

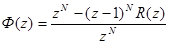
Полюсы Ф(z) могут возникать как :

— нули знаменателя Z=0

— полюсы числителя, так как R(z)-многочлен от Z, то это может быть только Z=0

Таким образом, при сделанных предложениях, Ф(z) имеет единственный полюс Z=0. Характеристическое уравнение имеет вид:

Подставив (6) и (4) в (3) получим

E(z)=A(z)R(z) — это Z-преобразование ошибки.

При этом, так как A(z) и R(z) -полиномы от Z, то E(z) тоже полином от Z и следовательно E(z) имеет конечное число членов при разложении в ряд по степеням Z. Таким образом, пр исделанных предложениях сигнал ошибки сводится к нулю за конечное число периодов квантования.

Таким образом, синтез цифрового регулятора может проводиться так

R(z)®Ф(z)®D(z)

При этом необходимо иметь физически реализуемую ПФ. Это можно проконтролировать при выборе Ф(z)

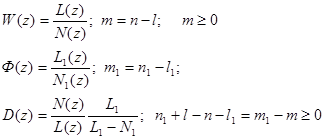
разность степеней числителя и знаменателя не меньше, чем у W(z), это необходимо учитывать при определении Ф(z). Вернемся к соотношению(6). N определяется типом входного сигнала. Тогда

N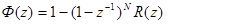

ступенчатый сигнал 1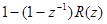

линейный 2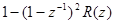

парабола 3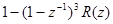

Видно, что при этом для ступенчатого сигнала минимальное время установления е=0 составляет один такт, для линейного — 2 такта и т.д.

Рассмотренный алгоритм определения D(z) имеет ряд особенностей:

1. Если W(z) имеет нули на единичной окружности или вне ее, то будет нужен енустойчивый регулятор. Этот случай нужно рассматривать отдельно

2. В таблице m=1 и должно быть, чтобы m<=1

Таким образом: если есть такие нули или m>1, то R(z) не может быть 1

Пример:

Пусть

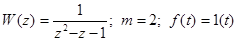
Нельзя взять Ф(z)=1/z из таблицы

Попробуем взять 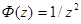, тогда

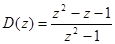
При этом

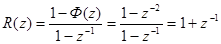
и процесс заканчивается за два такта.

В общем случае при заданном входе, определяющем N, минимальное число переиодов квантования, составляющих переходный процесс, равно

N+m-1