Реализация интегрирующих цифровых фильтров.

Перед решением общей задачи дискретизации аналогового прототипа рассмотрим предварительно реализацию интегрирующих цифровых фильтров. Уравнение непрерывного аналога имеет вид

.

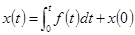Применяя для численного интегрирования метод прямоугольников, получим

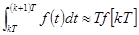
и тогда

.

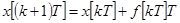Разностному уравнению соответствует передаточная функция

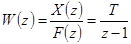. (114)

Применяя вместо формулы прямоугольников формулу трапеций, получим

,

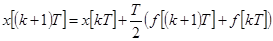при этом

. (115)

Логарифмические частотные характеристики цифрового фильтра (115) представлены на рис.46, откуда видно, что ЛАФЧХ непрерывного и дискретного корректирующих устройств совпадают только в диапазоне низких частот. Отметим, что возможно применение более точных формул численного интегрирования, дающих лучшее приближение к непрерывному звену,

Рассмотрим задачу реализации непрерывного корректирующего устройства, заданного своей передаточной функцией

.

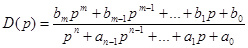с помощью цифрового фильтра. Один из способов ее решения [5] состоит в замене непрерывного интегратора цифровым с передаточной функцией (114) или (115). При этом передаточную функцию D(p) записывают по отрицательным степеням P , т.е.

.

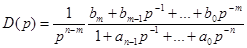Передаточная функция цифрового фильтра находится с помощью перехода 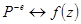, где 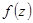- определенная функция, соответствующая тому или иному способу численного интегрирования. Например, при использовании формулы (115)

,

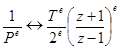и тогда

.

Возможно применение других форм 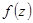, при которых цифровой фильтр будет иметь иную z -передаточную функцию D(z).