Способ прямого программирования.

Рассмотрим переход от описания импульсной системы с помощью Z-передаточных функций к описанию с помощью переменных состояния. Как уже отмечалось, выбор переменных состояния не является единственным, и определяется выбором соответствующего базиса. Практически удобным приемом выбора переменных состояния является составление схем моделирования дискретных систем. Схемы включают в себя элементы задержки на такт и сумматоры. Пpи выбope пepeмeнныx cocтoяния импульсных систем за них удобно принимать выходы элементов задержки на такт.

Рассмотрим три способа перехода от Z-передаточной функции дискретной системы к уравнениям (57), (58): способы прямого программирования, последовательного программирования и параллельного программирования на примере звена второго порядка с одним входом и одним выходом и передаточной функцией

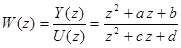
При способе прямого программирования, разделив числитель и знаменатель передаточной функции на 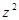(в общем случае на 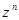), получим

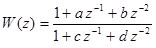(60)

По определению передаточной функции

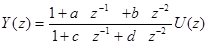
Введем новую переменную e[kT], Z -преобразование которой имеет вид

.

Тогда

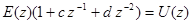
или

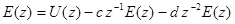
В соответствии с выражением (60) составляем схему моделирования (рис.35). При этом учитываем, что множитель 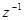соответствует задержке переменной на один такт квантования.

Рис. 35

Уравнения состояния системы можно получить, записывая соотношения, связывающие координаты на выходах элементов задержки. В итоге имеем

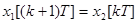
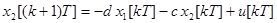. (61)

Так как

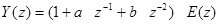
и при этом

,

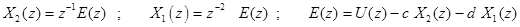то для выходной переменной y[kT] получим уравнение

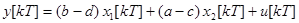(62)

Таким образом, уравнения (57), (58) принимают вид (61). (62), а матрицы Ф, Н, C, D определяются выражениями

.

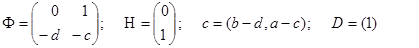Запись системы уравнений (61) для общего случая не представляет сложности. При этом матрица Ф будет иметь структуру, аналогичную собственной матрице системы дифференциальных уравнений, записанных в первой нормальной форме Коши.