Пространство состояний дискретной системы

Метод пространства состояний является весьма эффективным инструментом исследования дискретных САУ, получившим в настоящее время широкое распространение. Ниже излагаются некоторые аспекты его приложения к анализу импульсных систем. При этом используются сведения из теории решетчатых функций и разностных уравнений, рассматриваемые в курсе "Математические основы ТАУ".

Пусть процессы в дискретной системе характеризуются переменными 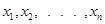, которые изменяются под влиянием входных воздействий 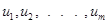. Если набор переменных 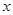оказывается таким, что знание их значений в некоторый начальный момент вместе с заданием входных воздействий 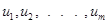оказывается достаточным для того, чтобы определить последующие значения 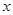, то набор можно назвать полным. Полный набор переменных может обладать избыточной информацией о поведении системы, некоторые переменные могут оказаться излишними, дублировать другие. Переменные 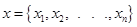, принадлежащие минимальному полному набору, назовем переменными состояния системы. Таким образом, состояние системы может быть охарактеризовано как минимальная информация о системе, достаточная для описания ее настоящего и будущего при известном входе.

Если при этом переменные состояния принадлежат n-мерному евклидову пространству X , то пространство X называют пространством состояния системы.

Число переменных состояния обычно превышает число реально интересующих нас физических величин, по которым оценивается качество работы системы. Переменные состояния необязательно являются физическими измеряемыми переменными, характеризующими отдельные элементы системы. В общем случае переменные состояния - абстрактные переменные, хотя они, конечно, могут и совпадать с выходными переменными системы y . Выходные переменные системы y выражаются через переменные состояния системы, т.е.

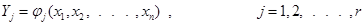
Для линейных систем уравнения, описывающие изменение переменных состояния, и функции 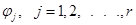являются линейными.

Представление системы в переменных состояния неоднозначно. Существует бесчисленное число минимальных полных наборов переменных состояния, равнозначных с точки зрения математического описания системы.