АНАЛИЗ РАЗМЕРНОСТЕЙ И МЕТОД АНАЛОГИЙ
Анализ размерностей, теория подобия, моделирование, а также метод аналогии различных явлений позволяют, наряду с правильной постановкой и проведением экспериментов, ускорить вычислительные и другие работы. Однако в теоретических основах бурения нефтяных и газовых скважин этот метод широко не применяется. В то же время в теоретических основах разработки нефтяных и газовых залежей эти средства сравнительно широко применяются.
Для правильной постановки экспериментов, обработки получаемых результатов и обобщений нужно проводить количественно-теоретический анализ. В этом случае уменьшается количество опытов, результаты которых выражаются в безразмерных параметрах. В гидродинамике, в частности, эти параметры определяются, как соотношение сил.
Обычно различают величины размерные и безразмерные. Примерами размерных величин являются скорость, давление, вязкость, предельное напряжение сдвига, длина, время и др.
Отношения длины к ее диаметру, сил вязкости к предельному напряжению сдвига и т. д. являются безразмерными величинами. Анализ теории размерностей позволяет в уравнениях путем перехода от размерных переменных к безразмерным уменьшить число переменных. Допустим, что дано следующее квадратное уравнение:
ax2 + bx+c = 0,
где безразмерный х зависит от коэффициентов а, bи с, имеющих одинаковые размерности.
Если все члены уравнения разделить на с, то уравнение примет вид
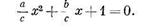
Как видно из уравнения, переменная х зависит от 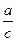 и
и 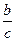 , т. е.
, т. е.
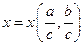 . Следовательно, запись уравнения в безразмерном виде
. Следовательно, запись уравнения в безразмерном виде
позволяет уменьшить число переменных с трех до двух. Если уравнение неизвестно или необходимо определить вид функциональной зависимости, то вместо изменения а и bизменим отношения 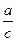 и
и 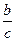 . Таким образом, не только уменьшается число переменных, но и при наименьших затратах времени и труда достигается возможность проведения эксперимента. Допустим, что для постановки эксперимента требуется изменение величин
. Таким образом, не только уменьшается число переменных, но и при наименьших затратах времени и труда достигается возможность проведения эксперимента. Допустим, что для постановки эксперимента требуется изменение величин 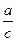 и
и 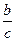 . Если во время экспериментирования величину с легко изменить, то, изменив величину с, можно изменить величины
. Если во время экспериментирования величину с легко изменить, то, изменив величину с, можно изменить величины 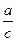 и
и 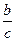 (при этом величины а и bостаются постоянными), и, наоборот, если трудно изменить величину с при экспериментировании, то, изменив величины
(при этом величины а и bостаются постоянными), и, наоборот, если трудно изменить величину с при экспериментировании, то, изменив величины 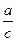 и
и 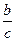 , можно изменить величины a и b. Если же
, можно изменить величины a и b. Если же
при проведении экспериментов сложно изменить величины b ис, то изменением одной из них можно достигнуть изменения отношения величин.
Физические основы связывают величины определенными зависимостями. Поэтому, если для некоторых величин будут выбраны размерности, то на основании соответствующих формул могут быть получены размерности других величин. Зависимость между физическими величинами позволяет выбрать такую основную систему размерностей, что для измерения в этой системе механических величин достаточен произвольный выбор трех размерностей.
Во многих случаях в технике единицы длины L, времени Т и силы F принимаются за основные единицы. Однако среди единиц измерения вязкость 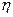 , скорость v и плотность
, скорость v и плотность 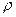 также могут быть приняты за основные. Такие величины называются величинами с независимыми размерностями (см. ниже).
также могут быть приняты за основные. Такие величины называются величинами с независимыми размерностями (см. ниже).
В настоящее время принята международная система единиц СИ, в которой размерность длины 1 м, массы — 1 кг и времени — 1 сек.
Если обозначить независимые размерности длины, времени и силы соответственно через L, Т и F, то широко применяемые в гидромеханике величины будут иметь следующие размерности:
скорость
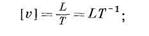

Если для математического описания нельзя составить дифференциальное уравнение или другую математическую зависимость, то, применяя теорию размерностей, можно описать физическое явление без уравнения, описывающего процесс. Но для этого необходимо знать поясняющие данное явление начальное и граничные условия. Применение для этих целей 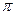 -теоремы (теоремы Букингема) позволяет выявить основные безразмерные параметры, характеризующие рассматриваемое явление.
-теоремы (теоремы Букингема) позволяет выявить основные безразмерные параметры, характеризующие рассматриваемое явление.
Предположим, что безразмерная величина а зависит от не зависящих друг от друга переменных величин а1: ..., ап
а = а(а1, а2, a3, . . ., ат, ат+1, . . ., ап).
Функциональная зависимость обычно записывается в виде 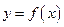 ; при большом количестве зависимостей
; при большом количестве зависимостей 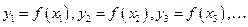 . Знаки функции должны приниматься различными. Проще зависимости изображаются так:
. Знаки функции должны приниматься различными. Проще зависимости изображаются так: 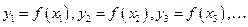
Допустим, что среди этих размерных величин число величин с независимыми размерностями равно т. В механике и технике их не может быть более трех. За независимые размерности принимаются длина L, время Т, сила F или же их степенная комбинация, из которой могут быть получены L, Т и F, например:
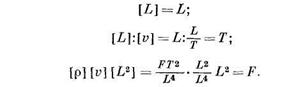
В уравнение входят n+1 размерных величин. На основании 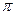 л-теоремы связь между п + 1 размерными единицами может быть осуществлена п + 1 — m безразмерными параметрами, состоящими из п + 1 размерных величин.
л-теоремы связь между п + 1 размерными единицами может быть осуществлена п + 1 — m безразмерными параметрами, состоящими из п + 1 размерных величин.
Тогда безразмерные параметры можно записать

Здесь показатели т1,т2, ..., mk; p1 р2, ,.., pk; g1 g2..., gk выбираются так, чтобы параметры 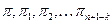 получились в безразмерном виде.
получились в безразмерном виде.
Применение 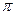 -теоремы поясним на конкретном примере. Предположим, что вместо величины
-теоремы поясним на конкретном примере. Предположим, что вместо величины 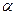 дана
дана 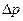 , а вместо величин с независимыми размерностями даны
, а вместо величин с независимыми размерностями даны 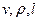 . Тогда получим
. Тогда получим
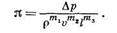
Так как в этой формуле левая часть 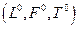 безразмерная, то и правая часть должна быть безразмерной, т. е.
безразмерная, то и правая часть должна быть безразмерной, т. е.
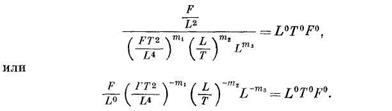
Тогда, приравнивая показатели степени при L, Т и F, получаем:
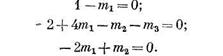
|
Решения этой системы трех линейных уравнений будут следующие:
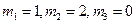
Следовательно, безразмерный параметр можно представить ввиде
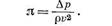
Это выражение представляет собой отношение давления и инерции и называется параметром Эйлера.
При использовании теории размерности используются физические и математические соображения.
Рассмотрим стационарное движение несжимаемой вязко-пластической жидкости в цилиндрической трубе. Перепад давления на концах трубопровода зависит от длины и диаметра трубы, структурной вязкости, предельного напряжения сдвига, плотности жидкости, а также от ускорения силы тяжести и скорости движения. При движении сжимаемой жидкости в уравнение должен войти не перепад давления, а абсолютные значения давлений, действующих на концах трубы. Для рассматриваемого случая физическое уравнение имеет вид
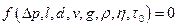 , или
, или
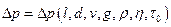 .
.
Так как число независимых равно трем, то, используя 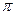 -теорему, можем вывести пять безразмерных параметров. В данном случае в качестве величин с независимыми размерностями могут быть выбраны следующие:
-теорему, можем вывести пять безразмерных параметров. В данном случае в качестве величин с независимыми размерностями могут быть выбраны следующие: 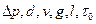 и т. д.
и т. д.
Выше было отмечено, что в каждом варианте величины с независимыми размерностями нужно выбирать так, чтобы их степенные комбинации дали бы возможность получить размерности длины L, силы F, времени Т. Теперь для принятых вариантов проверим это условие.
Так как в первом варианте давление, диаметр и скорость приняты за основные, то, комбинируя их, будем стремиться получить размерности L, F и Т.
Найдем размерность длины
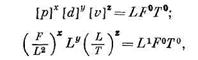
откуда 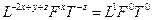
Следовательно, 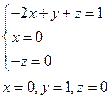
.
Таким образом, для получения размерности длины нужно принять следующую комбинацию р, d и v:
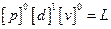 .
.
Найдем размерность силы:
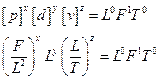 ,
,
откуда
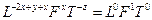
Следовательно,
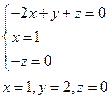 ;
;
т. е. для получения размерности силы нужно воспользоваться следующей комбинацией 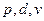 :
:
 .
.
Найдем размерность времени
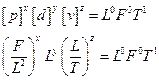 ,
,
откуда
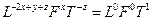
Следовательно,
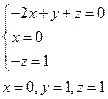 .
.
Размерность времени получим из приводимой ниже комбинации р, d и v:
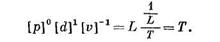
В каждом варианте комбинации этих величин выбираются так, чтобы в результате можно было бы получить безразмерный параметр. Теперь для каждого из двух вариантов выведем безразмерные параметры.
Вариант 1. Комбинации трех величин, принятых при выводе безразмерных параметров 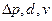 , должны быть выбраны так, чтобы можно было получить размерности остальных величин, а затем в результате деления привести полученную величину к безразмерному виду.
, должны быть выбраны так, чтобы можно было получить размерности остальных величин, а затем в результате деления привести полученную величину к безразмерному виду.
Для величины 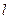 можем записать:
можем записать:


|

|
| Таким образом, получим пятый безразмерный параметр в виде |

|
Таким образом, получим четвертый безразмерный параметр в виде
Здесь для стационарного движения вязко-пластических жидкостей получены параметры Eu, Fr, La' и La".
Аналогично, если вывести безразмерные параметры для 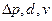 , то получим
, то получим
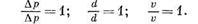
Ввиду того, что из восьми величин, входящих в уравнение, три приняты за независимые переменные, число безразмерных параметров уменьшится на число независимых переменных, т. е. получим п — т = 8—3 = 5 безразмерных параметров.
Вариант 2. Принимая размерные величины 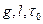 за основные и выводя из
за основные и выводя из 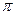 -теоремы безразмерные параметры, получаем следующие выражения:
-теоремы безразмерные параметры, получаем следующие выражения:
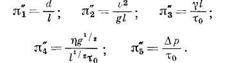
Сопоставим их с параметрами варианта I:
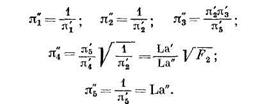
Ввиду того,что, что искомая величина 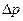 входит входит в параметр Eu, то результаты опытов представлены в виде
входит входит в параметр Eu, то результаты опытов представлены в виде
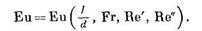
Так как величина 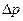 входит в параметрEu, остальные три параметра выбираем так, чтобы там искомая величина
входит в параметрEu, остальные три параметра выбираем так, чтобы там искомая величина 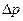 не участвовала.
не участвовала.
Уравнение можно выразить и с помощью параметра Лагранжа, в котором участвует 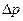 , т. е.
, т. е.
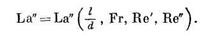
Это уравнение применимо для стационарного движения; если же движение нестационарное, необходимо принять во внимание и параметр Струхаля.
При горизонтальном положении трубы силы тяжести не оказывают влияния на движение, поэтому g во внимание не принимается.
Так как при изотермическом движении физические свойства ;ьидкости по длине трубы не меняются, расход и сечение остаются постоянными, то потери давления, приходящиеся на единицу длины (из уравнения неразрывности), бывают разными. В этом случае характерным является 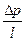 .Например, если будем знать потери давления, соответствующие 100 м длины, то можно определить потери давления на 200, 300 м и т. д. Здесь начальные и концевые участки во внимание не принимаются. Тогда перепад давления па единицу длины может быть выражен как
.Например, если будем знать потери давления, соответствующие 100 м длины, то можно определить потери давления на 200, 300 м и т. д. Здесь начальные и концевые участки во внимание не принимаются. Тогда перепад давления па единицу длины может быть выражен как
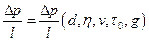 .
.
Так как определяется 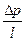 , то параметр
, то параметр 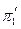 отпадает и параметр Эйлера записывается в виде
отпадает и параметр Эйлера записывается в виде
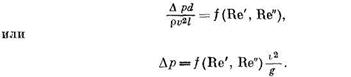
Для вязких жидкостей аналогичное уравнение, выведенное независимо друг от друга Дарси и Вейсбахом, называется уравнением Дарси — Вейсбаха.
Таким образом,
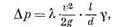
где 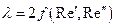 — коэффициент гидравлических сопротивлений.
— коэффициент гидравлических сопротивлений.
Рассмотрим уравнение длинной двухпроводной линии [9]. Двухпроводная линия представлена системой с равномерно распределенными утечками, индуктивностями, сопротивлениями и емкостями. Разность потенциалов U и сил тока i в сечениях х и 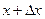 определяется на основании закона Кирхгофа, записанного для процесса, протекающего на отрезке
определяется на основании закона Кирхгофа, записанного для процесса, протекающего на отрезке 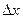 в промежуток времени
в промежуток времени 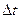 . Разность U(x, t) - U(х + Ах, t) определяет разность потенциалов на индук-тивиостях и омических сопротивлениях
. Разность U(x, t) - U(х + Ах, t) определяет разность потенциалов на индук-тивиостях и омических сопротивлениях
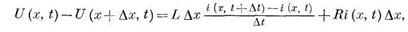
где L и R — соответственно индуктивность и омическое сопротивление на единицу длины.
Первый член правой части, характеризующий изменение э. д. с. на индуктивностях, определяется изменением силы тока во времени. Второй член — разность потенциалов, которая рассчитывается по закону Ома.
Второе уравнение — баланс силы тока, определяемый конденсатором и утечкой, т. е.
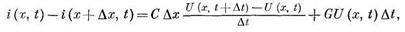
' где С — емкость, приходящаяся на единицу длины; G- — проводимость на единицу длины.
Первый член правой части — сила тока, проходящего через конденсатор и характеризуемого изменением в течение времени разностью потенциалов. Второй член — сила тока — утечка, определяемая по закону Ома.
Приведенные два уравнения — конечно-разностные уравнения длинной двухпроводной линии. Переходя к пределу при 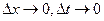 , можно получить:
, можно получить:
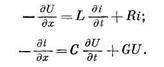
Эта система уравнения при G = 0 вполне аналогична дифференциальным уравнениям движения капельной жидкости в трубопроводе при 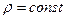 .
.
Рассмотрим неустановившееся движение реальной среды в гори-зонтальной круглой цилиндрической трубе. В этом случае одно гремя релаксации характеризует пестационарность вдоль оси, дру-юе — вдоль сечения. Предполагается, что второе пренебрежимо -тало по сравнению с первым. Поэтому исследуется нестационар-юсть, развивающаяся вдоль оси трубы, т. е. рассматривается ква-зиодномерное движение, характеризуемое параметрами, осреднен-м.ши по сечению. Предполагается, что жидкость малосжимаемая, т. е. изменение ее скорости вдоль оси мало. В сечении 1—1 (см. Рис. 9) среднее давление обозначается через р (х, t), а в сечении 2—2 — через 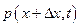 .
.
Касательное напряжение обозначается через 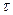 . Тогда сила тре-шя, действующая на боковую поверхность элементарного круглого цилиндра, будет
. Тогда сила тре-шя, действующая на боковую поверхность элементарного круглого цилиндра, будет 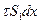 , где S1 — смоченный периметр.
, где S1 — смоченный периметр.
В уравнении движения «местная скорость» приближенно заменяется средней по сечению скоростью v, но это не влияет на конечный результат.
Сумма сил сопротивления и давления равна 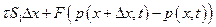 , где F — площадь поперечного сечения.
, где F — площадь поперечного сечения.
Переходя к пределу, получаем
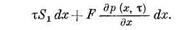
Абсолютную величину силы инерции выразим через 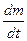 , где
, где
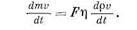
|
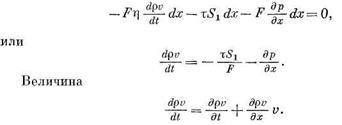
|
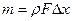 — масса среды в отсеке 1—1, 2—2 трубы. Тогда в пределе. На основании принципа Д'Аламбера
— масса среды в отсеке 1—1, 2—2 трубы. Тогда в пределе. На основании принципа Д'Аламбера
Ввиду того, что скорость мало изменяется по длине трубы, вторим членом этого равенства но сравнению с первым можно пренебречь, т.е. 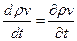
Сформулируем более полно условия, при которых можно пренебречь вторым членом но сравнению с первым. Первый член 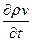 имеет порядок
имеет порядок 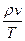 , второй
, второй 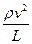 (L — характерный размер, в данном случае длина трубопровода, Т — характерное время, в качестве которого может быть принято время релаксации). Вторым членом можно пренебречь по сравнению с первым при условии
(L — характерный размер, в данном случае длина трубопровода, Т — характерное время, в качестве которого может быть принято время релаксации). Вторым членом можно пренебречь по сравнению с первым при условии

Параметр 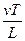 безразмерный. Оценим величину этого параметра для магистрального трубопровода:
безразмерный. Оценим величину этого параметра для магистрального трубопровода: 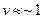 1 м/сек;
1 м/сек; 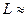 100 км.
100 км.
Если принять, что время релаксации порядка нескольких часов соответствует времени практического достижения стационарного
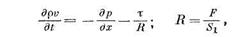
где R — гидравлический радиус.
Уравнение неразрывности запишем в виде
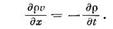
режима, то получим 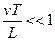 . Тогда
. Тогда
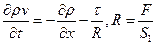
где R гидраврический радиус
Уравнение неразрывности запишем в виде
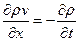
Для изотермического движения принимается уравнение состояния
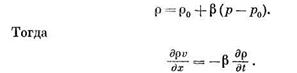
Вводя вместо 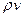 среднемассовую скорость w, можно записать
среднемассовую скорость w, можно записать
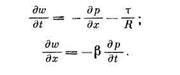
Из анализа размерностей нетрудно установить, что при ламинарном режиме 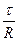 пропорционально средней скорости в первой степени,
пропорционально средней скорости в первой степени,
а при турбулентном режиме — квадрату скорости.
Необходимо еще раз отметить, что здесь мы воспользовались принципом квазистационарности, т. е. силы сопротивления определяли по формулам для стационарного режима. Принимая 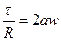 , находим
, находим
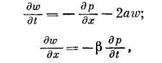
где 2а — коэффициент сопротивления.
Из этих двух уравнений можно получить одно
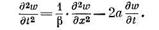
Рассмотрим, как, используя соображения размерности, можно упростить уравнение. Переищем к безразмерным переменным:
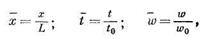
где L, t0 и w0 — характерные величины.
В качестве L принималась длина трубопровода. Следовательно, в
безразмерных переменных
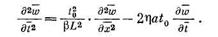
Из условия 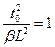 определяется
определяется 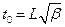 . Окончательно
. Окончательно
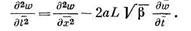
Если коэффициент при члене 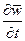 достаточно большой, то можно пренебречь силой инерции
достаточно большой, то можно пренебречь силой инерции 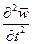 по сравнению с силой сопротивления
по сравнению с силой сопротивления 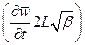 .
.
Таким образом, перепад давления расходуется только лишь на преодоление сил сопротивления. В этом случае уравнение принимает вид
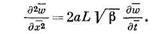
Естественно, что принятое предположение оправдывается для трубопроводов очень большой длины и при движении в них жидкости очень большой вязкости. При определении пускового давления в трубопроводах и в скважине можно пренебречь силой инерции
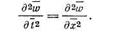
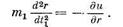
|
Уровень, который может быть принят как достаточно большой, определяется на основании сопоставимых расчетов. Соображения подобия позволяют, не решая уравнения, получить некоторую информацию. Например, второй закон Ньютона для частного случая потенциального силового поля [2] можно записать в виде
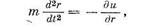
приняв 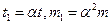 , можно получить
, можно получить 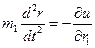
Следовательно, если уменьшить массу точки в 25 раз, то на прохождение орбиты потребуется времени в пять раз меньше.
Среди различных явлений, встречаемых в природе, выявлено много математических аналогий. За последние десятилетия в практике применяются лабораторные исследования и проекты, основанные на электрических, магнитных, электродинамических, электромагнитных, тепловых, звуковых, оптико-механических, магнитно-оптических и других аналогиях и на теории моделирования. Электромоделирование различных физических явлений широко используется в теории фильтрации, гидравлике, гидродинамике, строительстве, теплотехнике, теории упругости, механике грунтов, теории механизмов, акустике, теории автоматического регулирования, а также в других областях науки и техники.
В современном гидротехническом строительстве при строительстве больших и сложных гидротехнических объектов требуется проводить сложные исследования по фильтрации. Теоретическое исследование этих вопросов очень сложно, а иногда и неразрешимо. Эти сложные вопросы очень легко разрешаются с помощью метода ЭГДА (электрогидродинамическая аналогия), в том числе разрешаются многие задачи, относящиеся к фильтрации нефти, газа и газированных жидкостей.
Применение метода ЭГДА при исследовании фильтрации почвенных вод под гидротехнические сооружения впервые в 1918 г. было предложено и теоретически обосновано академиком Н. Н. Павловским. Метод ЭГДА также широко используется в различных областях научных исследований.
Применение центробежного моделирования дает хорошие результаты при решении следующих задач, относящихся к статике и динамике пород: определение прочности земляных строительных откосов; определение прочности валов и других строительных фундаментов; распределение напряжений в породах и на контакте строительных поверхностей с породой; оседание зданий; фильтрация воды в породе и влияние фильтрации па породы; определение в связанных породах сил трения и сцепления и т. д.
Ниже покажем два простых примера, относящихся к аналогии.
Аналогия между электрическими и механическими явлениями
В замкнутую цепь (рис. 25) включены конденсатор с емкостью С, омическое сопротивление R, катушка самоиндукции L и ключ К.
Через цепь проходит электрический ток I. Для последовательной цепи, как известно из закона Кирхгофа, разность потенциалов будет состоять из суммы разности напряжений на
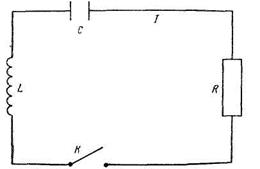
Рис.25
омическом сопротивлении, конденсаторе и катушке. Эти три составляющие рассчитываются следующим образом:
а) в результате самоиндукции разность напряжений равняется произведению коэффициента самоиндукции 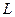 на скорость изменения тока, т. е.
на скорость изменения тока, т. е. 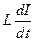 ;
;
б) разность напряжений, связанных с омическим сопротивлением, равна произведению RI (закон Ома);
в) разность напряжений на конденсаторе (по определению)
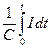 .
.
о
Таким образом, дифференциальное уравнение, описывающее явление, запишем в виде
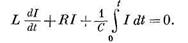
При решении этого дифференциального уравнения второго порядка для нахождения двух постоянных должны быть заданы два условия. Например, в начальный момент времени t = t0 задаются
утопия 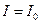 и
и 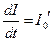 .
.
Остановимся на условиях, необходимых для решения уравнений. Если явление описывается обыкновенным дифференциальным уравнением n-го порядка, т. е. в уравнении искомая функция зависит только от одного аргумента (п — самый высокий порядок производной, входящей в уравнение, — целое число, которое может равняться единице или более), то в результате его решения должно получиться п произвольных постоянных. Для нахождения их должны быть заданы п условий. Эти условия, зависящие от характера изучаемого явления, могут быть заданы различными способами.
1. При определенном значении аргумента задается функция и ее п - 1 производные. Например, если в заданном уравнении третьего порядка искомая функция зависит от времени, то для определенного
значения времени должны быть даны функции и ее первая и вторая производные.
Такая задача называется задачей с начальными условиями, или задачей Коши.
2. При определенных значениях аргументов задаются функции и их производные. Например, если иметь дифференциальное уравнение пятого порядка, то из двух значений аргументов при одном из них даются искомая функция и ее первая и вторая производные, а при другом значении — функция и ее третья производная. Здесь в зависимости от постановки задачи возможны также различные другие варианты.
Для приведенной электрической цепи граничные условия могут быть заданы так:
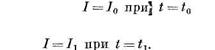
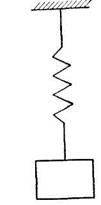
Рассмотрим механическую цепь, имеющую одну степень свободы. Напишем условие равновесия сил, действующих на пружину (рис. 26).
|
Рис. 26.
На пружину действуют активные силы тяжести и упругости и пассивная сила сопротивления.
Воспользовавшись принципом Д'Аламбера, условие равновесия запишем в виде
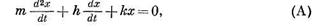
где т — масса; h — затухание колебания; к — коэффициент жесткости; х — перемещение.
В приводимом уравнении (А) первый член по абсолютному значению представляет силу инерции, второй — силу трения, а третий — силу упругости.
Уравнение механического колебания имеет тот же вид, что и уравнение, описывающее электрическое колебание. Следовательно, в указанных уравнениях аналогичными являются параметры: х — I,
т — L: h — R 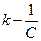 .
.
Перейдем к безразмерным величинам следующим образом:
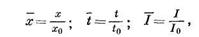
где t0 — начальное значение аргумента; х0 и I0 — начальные значения функции. Таким образом,
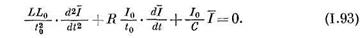
Если все члены уравнения разделить на 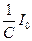 , to получим следующее уравнение с безразмерными коэффициентами:
, to получим следующее уравнение с безразмерными коэффициентами:
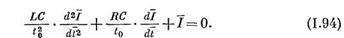
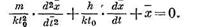
|
Аналогично уравнение механических колебаний можно записать в безразмерном виде
Напишем начальные условия для уравнения колебаний в электрической цепи в безразмерном виде:
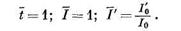
Начальные условия для уравнения механического колебание будут:
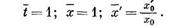
Для равенства вторых начальных условий должно быть удовлетворено следующее условие:

Теперь, пользуясь аналогией уравнений механического и элекричсского колебаний, перейдем от одного уравнения к другому.
Предположим, что для механического контура т, к и h заданы. И электрическом контуре при известных 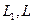 , задавшись
, задавшись 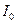 , можно найти
, можно найти 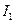 .
.
для идентичности уравнений описывающих механические и электрические колебания, необходимо
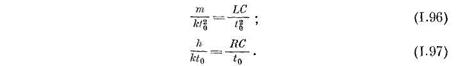
Тогда будут равны друг другу 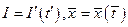 .
.
В уравнениях (1.93) и (1.94) для нахождения неизвестныхR, С, L нужно задаться одним из них. Например, задавшись значением С, можно найти R и L.
Для заданных начальных условий 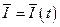 , чтобы в механической системе удовлетворить условию
, чтобы в механической системе удовлетворить условию 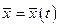 , рассмотрим выбор параметров электрического контура и начальных условий. Для этого
, рассмотрим выбор параметров электрического контура и начальных условий. Для этого 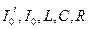 должны выбираться так, чтобы равенства (1.95) — (1.97) были удовлетворены. Например, задавшись значениями С и I'0, из этих трех уравнений можно найти I0, L и R. Выбор этих параметров зависит от места и условий опыта.
должны выбираться так, чтобы равенства (1.95) — (1.97) были удовлетворены. Например, задавшись значениями С и I'0, из этих трех уравнений можно найти I0, L и R. Выбор этих параметров зависит от места и условий опыта.
После нахождения этих параметров для установления зависимости I=I(t) собирается соответствующая электрическая цепь.
Гидравлическая аналогия при решении задач теплопередачи [15]
Аналитическое решение задач теплопередачи со сложными краевыми условиями и изменяющимися термическими коэффициентами (которые часто встречаются в практике) связано с большими трудностями. Применение же метода элементарных балансов связано с трудоемкими вычислительными операциями. В связи с этим созданы счетно-решающие приборы, основанные на аналогиях, облегчающих вычислительные операции. При использовании метода аналогии стремятся воспроизвести исследуемое данное явление на аналогичном явлении, которое описывается теми же математическими зависимостями, но более просто управляемом. При этом значительно облегчаются вычислительные работы.
Известны электрические модели нестационарных процессов теплопроводности (электроинтегратор Л. И. Гутенмахера); нашел применение и метод гидравлической аналогии, предложенный В. С. Лукьяновым.
Гидравлический интегратор В. С. Лукьянова основан на аналогии математических соотношений, описывающих распространение температуры в твердом теле и распределение напоров в воде, движущейся через гидравлические сопротивления при ламинарном режиме.
Основной принципиальной особенностью, определяющей устройство гидроинтегратора, является замена в гидравлическом поле равномерно распределенных параметров сосредоточенными, т. е. переход от поля к цепи с сосредоточенными параметрами. В связи с этим процесс воспроизведения непрорывного температурного поля с сосредоточенными параметрами представляет собой переход от решения дифференциальных уравнений к решению уравнения в конечных разностях.
Этот прибор состоит из основных элементов аналогии гидравлической цепи с сосредоточенными элементами сопротивлений и емкостей, а также специальных элементов, воспроизводящих выделение скрытой теплоты при изменении агрегатного состояния; устройства для задания граничных условий; приспособлений для измерения напора в узлах гидравлической цепи; устройства, обеспечивающего питание прибора водой.
Рассмотрим конкретный пример определения распределения температуры в многослойной стенке при одномерном тепловом потоке. Стенка задается размерами отдельных слоев и теплофи-зическими характеристиками материалов, т. е. объемными теплоемкостями ( 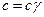 , где с — удельная теплопроводность тела;
, где с — удельная теплопроводность тела; 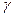 — объемный вес тела), и коэффициентами теплопроводности (рис. 27).
— объемный вес тела), и коэффициентами теплопроводности (рис. 27).
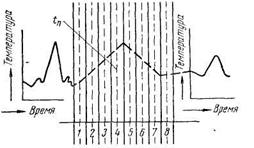
Рис. 27
Дано определенное начальное распределение температуры и произвольно выбранные воздействия температур наружных сред II тепловых потоков па поверхности стенки. Вначале составляется расчетная схема. Разбивают стенку на конечное число слоев. При этом допускается, что теплоемкость для каждого слоя сосредоточена в середине его и ограждается термическими сопротивлениями, равными половине толщины слоя.
Таким образом, расчетная схема представляет собой цепочку юплоемкостей с, разделенных между собой термическими сопротивлениями 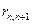 .
.
Теплоемкости крайних слоев отделены от наружной среды допол-пительным термическим сопротивлением теплоотдачи с поверхности. Процесс теплообмена элементарных слоев между собой и окружающей средой определяется следующей системой уравнений:
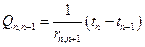 ; (1-98)
; (1-98)
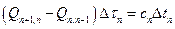 , (1-99)
, (1-99)
где 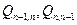 — количество тепла соответственно в слоях и,
— количество тепла соответственно в слоях и, 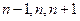 , t — температура соответствующих слоев;
, t — температура соответствующих слоев; 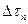 — время теплопроводности;
— время теплопроводности; 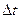 — разница температур. Гидравлическая аналогия осуществляется следующим образом. Составляется цепь из сосудов с определенными сечениями
— разница температур. Гидравлическая аналогия осуществляется следующим образом. Составляется цепь из сосудов с определенными сечениями 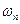 , соединенными между собой через гидравлическое сопротивление
, соединенными между собой через гидравлическое сопротивление 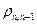 (рис. 28).
(рис. 28).
Число сосудов равно числу элементарных слоев. Крайние сосуды соединены с подвижными сосудами В1 и В2. Изменение уровней воды в сосудах будет определяться следующей системой уравнений:
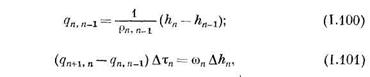
где q — расход жидкости; 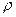 — коэффициент гидравлических сопротивлений; h — уровень жидкости в сосуде;
— коэффициент гидравлических сопротивлений; h — уровень жидкости в сосуде; 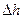 — разница уровней жидкости в сосудах.
— разница уровней жидкости в сосудах.
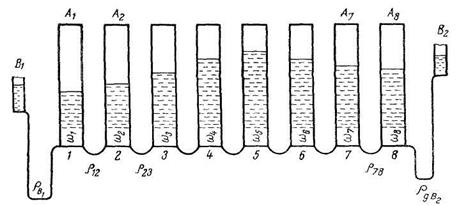
Рис. 28.
Расход жидкости q пропорционален разности уровней в сосудах 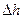 (аналог закона теплопроводности), а приращение содержания воды в сосуде
(аналог закона теплопроводности), а приращение содержания воды в сосуде 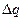 за время
за время 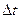 равно произведению площади сечения сосуда на приращение высоты уровня.
равно произведению площади сечения сосуда на приращение высоты уровня.
Уравнения (1.98) и (1.95) аналогичны уравнениям (1.100) и (1.101). Предположим, что цепь сосудов составлена так, что в ней величины 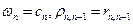 численно равны. Начальное распределение уровней h в соответствующем масштабе изображает начальное распределение температуры в центре элементарных слоев, а изменение уровней в подвижных сосудах происходит так же, как изменение температуры окружающих сред. Тогда уровень в сосудах будет изменяться аналогично изменению температуры в элементарных слоях. Если
численно равны. Начальное распределение уровней h в соответствующем масштабе изображает начальное распределение температуры в центре элементарных слоев, а изменение уровней в подвижных сосудах происходит так же, как изменение температуры окружающих сред. Тогда уровень в сосудах будет изменяться аналогично изменению температуры в элементарных слоях. Если 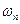 и
и 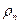 численно не равны
численно не равны 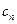 и
и 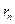 , а лишь пропорциональны им, то тепловой процесс также будет воспроизводиться на модели, по только в другом масштабе времени. Наличие такой возможности создает большие удобства, так как можно значительно ускорить иоспроизведение медленных и замедлить воспроизведение быстро протекающих процессов теплообмена. В этом случае перейти от гидравлической модели к исследуемому процессу можно посредством иыбора соответствующих масштабных соотношений.
, а лишь пропорциональны им, то тепловой процесс также будет воспроизводиться на модели, по только в другом масштабе времени. Наличие такой возможности создает большие удобства, так как можно значительно ускорить иоспроизведение медленных и замедлить воспроизведение быстро протекающих процессов теплообмена. В этом случае перейти от гидравлической модели к исследуемому процессу можно посредством иыбора соответствующих масштабных соотношений.
Если все величины, входящие в уравнения (1.98) — (1.101), выразить в безразмерных величинах, то система (1.98) и (1.99) будет подобна систем
Дата добавления: 2017-10-04; просмотров: 3904;











