АНАЛОГИ ШВИДКОСТЕЙ І ПРИСКОРЕНЬ
Аналітичне дослідження кінематики механізмів зручно вести з використанням аналогів швидкостей і прискорень. Це пояснюється тим, що для заданої кінематичної схеми механізму аналоги швидкостей і прискорень залежать тільки від узагальненої координати і не залежать від швидкості руху початкової ланки. Важливо зазначити, що аналоги швидкостей і прискорень дають змогу легко порівнювати закони руху ланок, а звідси й вибрати оптимальний варіант механізму для забезпечення заданих умов роботи.
Якщо кут повороту якої-небудь k-ї ланки задано як функція
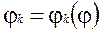 (1)
(1)
де 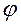 - кут повороту початкової ланки, то кутова швидкість wk цієї ланки може бути представлена так:
- кут повороту початкової ланки, то кутова швидкість wk цієї ланки може бути представлена так:
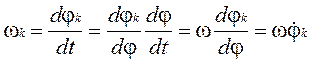 (2)
(2)
де, w - кутова швидкість початкової ланки [ 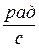 ];
];
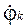 - безрозмірна кутова швидкість ланки (аналог кутової швидкості) чи передатна функція кутової швидкості.
- безрозмірна кутова швидкість ланки (аналог кутової швидкості) чи передатна функція кутової швидкості.
Отже, дійсна кутова швидкість wk дорівнює добутку кутової швидкості початкової ланки на аналог кутової швидкості ланки к.
Диференціюючи рівняння (2) за часом t маємо величину кутового прискорення ланки к:
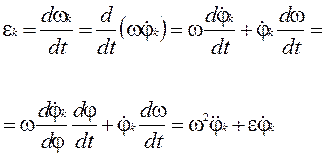 (3)
(3)
де 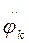 - аналог (передатна функція) кутового прискорення.
- аналог (передатна функція) кутового прискорення.
Аналогічно можуть бути отримані рівняння для швидкості і прискорення якої-небудь точки ланки k.
Нехай rm є радіус-вектор, який визначає положення точки m. Тоді швидкість точки m

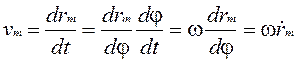 , (4)
, (4)
де,  - аналог швидкості точки m (має розмірність одиниць довжини).
- аналог швидкості точки m (має розмірність одиниць довжини).
Таким чином, дійсна швидкість точки m дорівнює добутку кутової швидкості початкової ланки на аналог швидкості точки m.
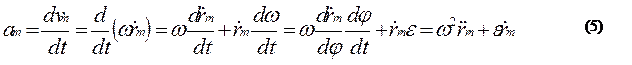 |
Диференціюючи вираз (4) за часом маємо величину прискорення а точки m:
де, 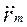 - аналог прискорення точки m (має розмірність одиниці довжини). Рух початкової ланки механізму при a = const називається перманентним чи основним рухом механізму. При цьому
- аналог прискорення точки m (має розмірність одиниці довжини). Рух початкової ланки механізму при a = const називається перманентним чи основним рухом механізму. При цьому 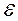 = 0, тоді:
= 0, тоді: 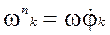 ; (10)
; (10)
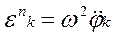 ; (11)
; (11)
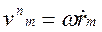 ; (12)
; (12)
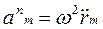 . (13)
. (13)
Якщо в рівностях (2 - 5) прийняти кутову швидкість ω =0, то кутові і лінійні швидкості ланок також дорівнюють нулю, а кутові і лінійні прискорення визначаємо за формулами:
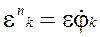 (14)
(14)
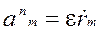 (15)
(15)
Рух ланки, описаний рівняннями (10), (11) називається початковим.
2. АНАЛІТИЧНЕ ДОСЛІДЖЕННЯ КІНЕМАТИКИ ЧОТИРИЛАНКОВОГО МЕХАНІЗМУ З ДВОПОВОДКОВОЮ СТРУКТУРНОЮ ГРУПОЮ II КЛАСУ 2 ПОРЯДКУ 1 ВИДУ
Розглянемо схему кривошипно-коромислового механізму.
Механізм може мати 2 схеми зібрання (рис.1, а, б) і утворюється вхідною ланкою АВ і структурною групою першого виду з трьома обертальними кінематичними парами В,С,D.
Рівняння замкненого векторного контуру, що утворений ланками механізму, має такий вигляд:
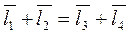 . (16)
. (16)
Проектуючи рівняння (4.1) на осі нерухомої системи координат ОХУ і враховуючи, що 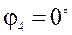 , маємо:
, маємо:
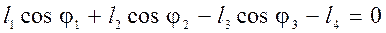 ; (17)
; (17)
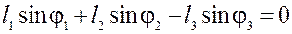
. 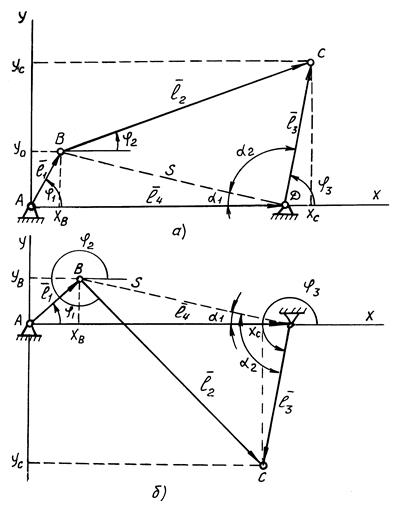
Рис.4.1 Схема кривошипно-коромислового механізму.
Координати точки В:
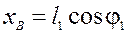 ; (18)
; (18)
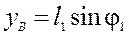 . (19)
. (19)
Задачу визначення положень механізму розв’язуємо поділом замкненого контуру АВСD на 2 трикутники: Δ АВD і Δ ВСD.
Розглянемо ΔАВD і ΔВСD для яких будуть справедливими такі залежності:
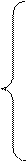
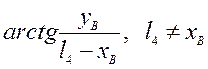 ;
;
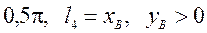 ;
;
a1=(20)
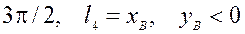 ;
;
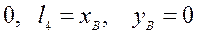 ;
;
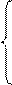
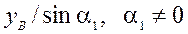 ;
;
S = (21)
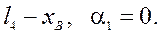
Напівпериметр Δ ВСD:
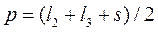 . (22)
. (22)
Радіус кола вписаного в Δ ВСD:
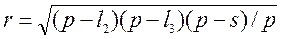 . (23)
. (23)
Допоміжний кут:
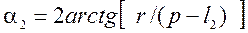 .
.
Кутова координата ланки DС:
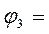
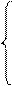
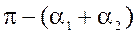 , для схеми (рис. 4.1 а); (24)
, для схеми (рис. 4.1 а); (24)
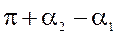 , для схеми (рис. 4.1 б), (25)
, для схеми (рис. 4.1 б), (25)
тоді координати точки С:
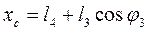 ; (26)
; (26)
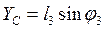 . (27)
. (27)

Кут φ 2 визначаємо через координати точок С і В:
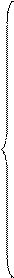
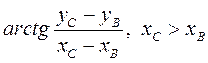 (сх. 1);
(сх. 1);
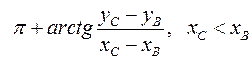 (сх. 1,2);
(сх. 1,2);
φ2 = 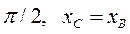 (сх. 2); (28)
(сх. 2); (28)
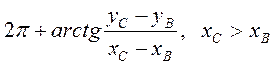 (сх. 2);
(сх. 2);
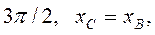 (сх. 2).
(сх. 2).
Для визначення аналогів швидкостей продиференціюємо систему (17) по узагальненій координаті φ1:
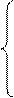
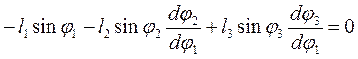 ; (29)
; (29)
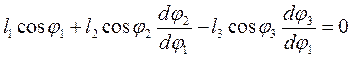 .
.
Позначимо: 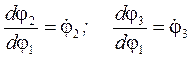 ,
,
де, 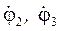 - аналоги кутових швидкостей відповідно 2 і 3 ланок, тоді систему (4.14) запишемо у такому вигляді:
- аналоги кутових швидкостей відповідно 2 і 3 ланок, тоді систему (4.14) запишемо у такому вигляді:
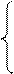
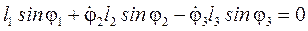 ; (30)
; (30)
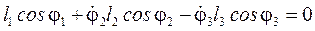 . (31)
. (31)
Від кутів, які входять у рівняння (4.15) віднімаємо спільний кут φ2 , що рівнозначно повороту системи координат ХАY на кут φ2:
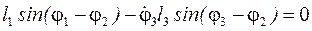 , (32)
, (32)
звідки:
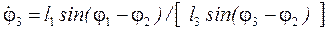 . (33)
. (33)
Після аналогічного перетворення рівняння (30) поворотом координатних осей на кут φ3 маємо:
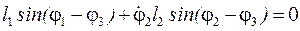 , (34)
, (34)
звідки:
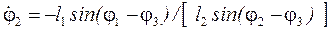 . (35)
. (35)
Для аналогів кутової швидкості можна записати:
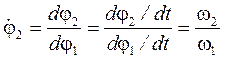 ; (36)
; (36)
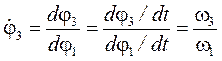 , (37)
, (37)
тоді кутові швидкості другої і третьої ланок:
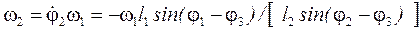 ; (38)
; (38)
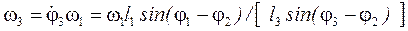 . (39)
. (39)
Лінійні швидкості точок:
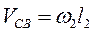 ; (40)
; (40)
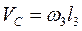 . (41)
. (41)
Для визначення кутових прискорень ланок 2 і 3 диференціюємо систему (30-31) по узагальненій координаті φ1:
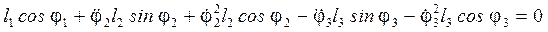 ; (42)
; (42)
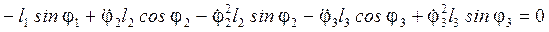 , (43)
, (43)
де 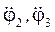 - аналоги кутових прискорень, які визначимо, якщо виконати перетворення координат послідовним поворотом їх осей на кути -φ2, -φ3.
- аналоги кутових прискорень, які визначимо, якщо виконати перетворення координат послідовним поворотом їх осей на кути -φ2, -φ3.
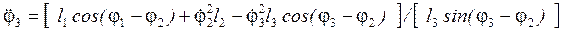 (44)
(44)
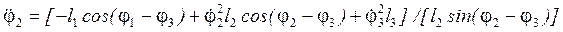 . (45)
. (45)
Кутові прискорення ланок:
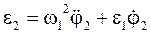 ; (46)
; (46)
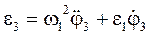 , (47)
, (47)
де 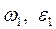 - задані кутова швидкість і кутове прискорення початкової ланки .
- задані кутова швидкість і кутове прискорення початкової ланки .
Прискорення точки С визначимо за формулою:
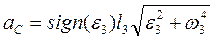 . (48)
. (48)
3. ЧОТИРИЛАНКОВИЙ МЕХАНІЗМ З ДВОПОВОДКОВОЮ СТРУКТУРНОЮ ГРУПОЮ ДРУГОГО ВИДУ( КРИВОШИПНО-ПОВЗУННИЙ МЕХАНІЗМ)
Механізм (рис. 9.3.).складається з початкової ланки 1 (кривошип) і двоповoдкової структурної групи 2 виду, яка включає ланки 2 (шатун) і 3 (повзун).
Рівняння замкненого векторного контуру механізму:
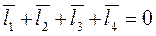 . (49)
. (49)
Проектуючи рівняння (4.34) на осі координат, отримуємо систему алгебраїчних рівнянь:
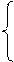
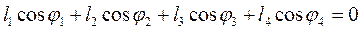 ; (50)
; (50)
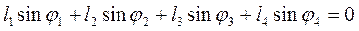 .
.
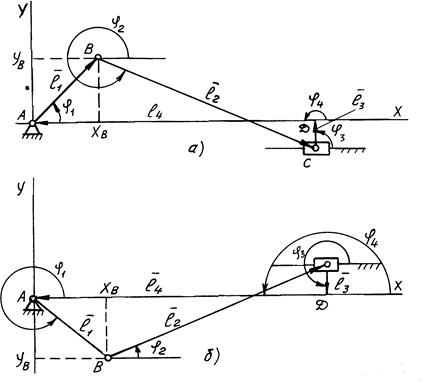
Рис. 9.3. Схема кривошипно-повзунного механізму.
Кути φ1 вимірюються від позитивного напрямку осі АХ до позитивного напрямку відповідного вектора 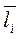 проти годинникової стрілки.
проти годинникової стрілки.
Для схеми (рис. 4.3,а) φ3 = 90º,φ4 = 180º; для схеми (рис. 4.3,б) φ3 = 270º,
φ4 = 180º, тоді система рівнянь (51) матиме вигляд:
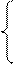
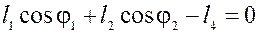 ;
;
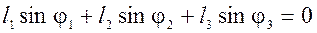 . (51)
. (51)
Координати точки В:
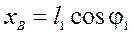 ; (52)
; (52)
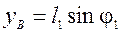 .
.
Для визначення координат точки С попередньо запишемо значення кута φ2:
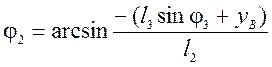 , (53)
, (53)
тоді:
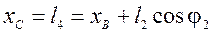 ; (54)
; (54)
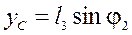 .
.
Для визначення швидкостей, кутової ланки 2, та лінійної точки С диференціюємо систему рівнянь (51) по узагальненій координаті φ1:
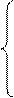
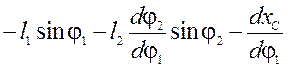 ; (55)
; (55)
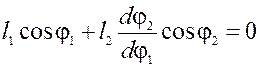 .
.
Позначимо: 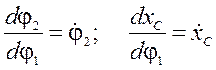 ,
,
де 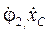 - аналоги кутової та лінійної швидкостей відповідно 2 та 3 ланок. Тоді система (55) матиме вигляд:
- аналоги кутової та лінійної швидкостей відповідно 2 та 3 ланок. Тоді система (55) матиме вигляд:
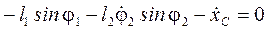 ; (56)
; (56)
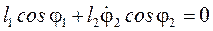 . (57)
. (57)
З рівняння (57) визначаємо:
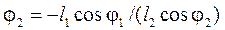 , (58)
, (58)
а з рівняння (56):
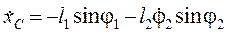 . (59)
. (59)
Аналогічно залежностям (36, 37) маємо:
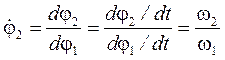 ; (60)
; (60)
 .
.
Тоді кутова швидкість другої ланки
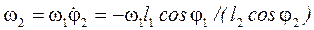 . (61)
. (61)
Лінійна швидкість точки С третьої ланки:
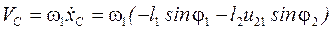 . (62)
. (62)
Для визначення лінійного прискорення точки С і кутового прискорення другої ланки продиференціюємо рівняння (56, 57) по узагальненій координаті φ1:
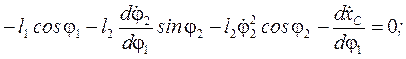 (63)
(63)
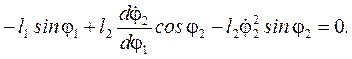
Позначимо 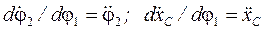 і перепишемо систему (4.48):
і перепишемо систему (4.48):
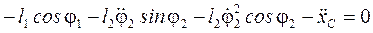 ; (64)
; (64)
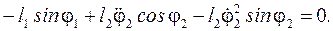 (65)
(65)
З рівняння (4.50) визначаємо 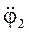 :
:
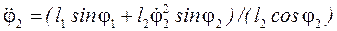 , (66)
, (66)
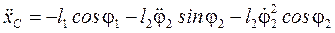 . (67)
. (67)
Аналогічно залежностям (4.31, 4.33) кутове прискорення другої ланки:
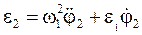 . (68)
. (68)
Лінійне прискорення точки С другої ланки:
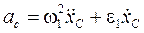 . (69)
. (69)
4. КУЛІСНИЙ МЕХАНІЗМ
Кулісний механізм (рис. 4.5) складається з вхідної ланки 1, яка утворює обертальну кінематичну пару з кулісним каменем 2. Кулісний камінь утворює поступальну кінематичну пару з кулісою 3. Вхідна ланка 1 і куліса 3 з’єднані зі стояком обертальними кінематичними парами А, С.
Розглянемо кулісний механізм у вигляді замкненого векторного контуру АВС, вектори якого утворені ланками 1, 2, 3.
Рівняння замкненого векторного контуру:
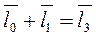 . (70)
. (70)
Cпроектувавши рівняння (4.55) на координатні осі YСХ, одержуємо систему алгебраїчних рівнянь:
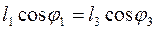 ; (71)
; (71)
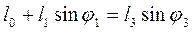 . (72)
. (72)
Для визначення напрямного кута φ3 розділимо рівняння (72) на (71), тоді маємо:
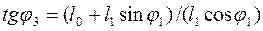 . (73)
. (73)
Визначимо довжину третьої ланки (куліси):
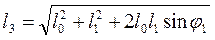 . (74)
. (74)
Для визначення швидкостей ланок механізму диференціюємо систему (71-72) по узагальненій координаті φ1:
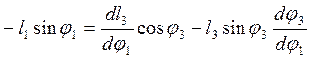 ; (75)
; (75)
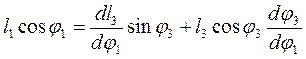 . (76)
. (76)
Позначимо 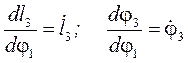 ,
,
де 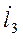 - аналог швидкості точки B3 відносно В2;
- аналог швидкості точки B3 відносно В2;
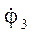 - аналог кутової швидкості ланки 3.
- аналог кутової швидкості ланки 3.
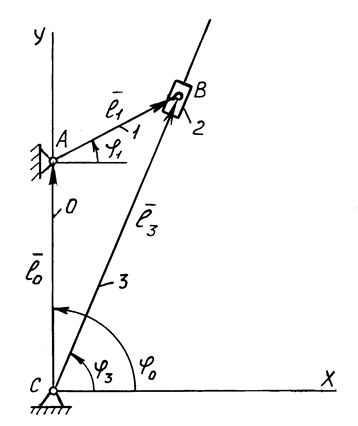
Рис. 4.5. Схема кулісного механізму.
Для визначення аналогів швидкостей від кутів, які входять в рівняння (75, 76) віднімаємо кут φ3, що еквівалентно повороту системи координат на такий самий кут:
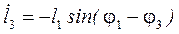 ;
;
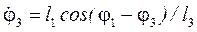 .
.
Аналогічно залежностям (62, 63) маємо:
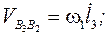 (77)
(77)
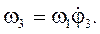 (78)
(78)
Для визначення аналогів кутових і лінійних прискорень ланок і точок механізму рівняння (75, 76), з урахуванням прийнятих позначень, диференціюємо по узагальненій координаті φ1:
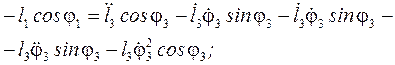 (79)
(79)
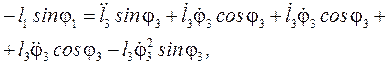 (80)
(80)
де, 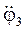 - аналог кутового прискорення ланки 3;
- аналог кутового прискорення ланки 3;
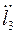 - аналог лінійного прискорення точки B3 відносно B2.
- аналог лінійного прискорення точки B3 відносно B2.
Віднімаємо від кутів, які входять в рівняння (79, 80) загальний кут φ3:
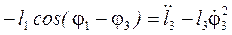 ; (81)
; (81)
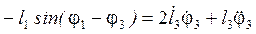 , (82)
, (82)
звідки:
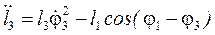 ;
;
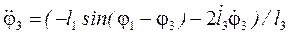 .
.
Аналогічно залежності (69) визначаємо відносне (релятивне) прискорення 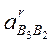 :
:
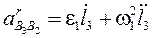 . (83)
. (83)
Прискорення Коріоліса 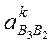 визначаємо за формулою:
визначаємо за формулою:
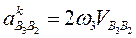 . (84)
. (84)
Кутове прискорення третьої ланки визначимо з рівняння (82):
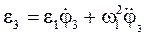 . (85)
. (85)
Тоді лінійне прискорення точки В3 визначимо аналогічно (48):
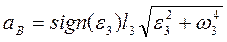 (86)
(86)
| <== предыдущая лекция | | | следующая лекция ==> |
| ВИЗНАЧЕННЯ ПРИСКОРЕНЬ ГРУПИ 2 КЛАСУ ПЕРШОГО ВИДУ | | | ДИНАМІЧНЕ ДОСЛІДЖЕННЯ МЕХАНІЗМІВ |
Дата добавления: 2016-06-15; просмотров: 3220;











