Учет экстраполятора при вычислении Z- передаточных функций.
Однако предположение о том, что передаточная функция W(p) ПНЧ есть дробно-рациональное выражение, не всегда выполняется. Как отмечалось ранее
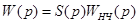 ,
,
где 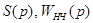 передаточные функции формирователя и собственно непрерывной части соответственно. Если
передаточные функции формирователя и собственно непрерывной части соответственно. Если 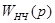 обычно является дробно-рациональной функцией, то
обычно является дробно-рациональной функцией, то 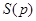 будет таковой лишь при некоторых упрощающих предположениях (см. [4] ). Обычно
будет таковой лишь при некоторых упрощающих предположениях (см. [4] ). Обычно 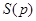 является трансцендентной функцией p, например, для экстраполятора нулевого порядка
является трансцендентной функцией p, например, для экстраполятора нулевого порядка
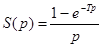 .
.
Рассмотрим этот случай и определим для него порядок нахождения Z-передаточной функции W(z). Пусть 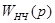 - дробно-рациональная функция
- дробно-рациональная функция
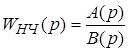 , (16)
, (16)
где 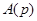 ,
, 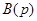 - многочлены степени m и n соответственно. Пусть
- многочлены степени m и n соответственно. Пусть  - полюсы передаточной функции (16). Считая, что все полюсы первого порядка, разложим выражение (16) на простейшие дроби:
- полюсы передаточной функции (16). Считая, что все полюсы первого порядка, разложим выражение (16) на простейшие дроби:
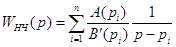 .
.
Тогда
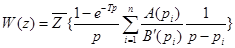
или
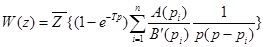 .
.
В соответствии со свойствами 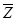 -преобразования множитель
-преобразования множитель 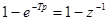 может быть вынесен за знак преобразования (см. курс “Математические основы ТАУ” или [6,прил.2]). Тогда
может быть вынесен за знак преобразования (см. курс “Математические основы ТАУ” или [6,прил.2]). Тогда
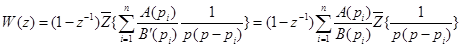 (17)
(17)
Найдем 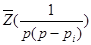 . Очевидно, что
. Очевидно, что
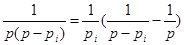 .
.
Пользуясь таблицей 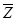 -преобразования с учетом теоремы линейности, получим
-преобразования с учетом теоремы линейности, получим
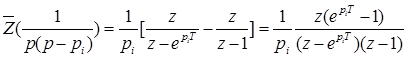 (18)
(18)
Подставив выражение (18) в формулу (17), найдем
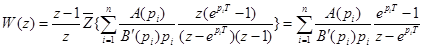 , (19)
, (19)
т.е. получена формула для вычисления Z-передаточной функции W(z) разомкнутой системы. Отметим, что при 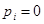 , а также при наличии кратных полюсов в формуле возникают неопределенности. Они могут раскрываться обычным способом, по правилу Лопиталя. Кроме того, формулу (17)) можно записать в виде
, а также при наличии кратных полюсов в формуле возникают неопределенности. Они могут раскрываться обычным способом, по правилу Лопиталя. Кроме того, формулу (17)) можно записать в виде
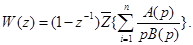
Здесь под знаком 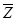 -преобразования стоит дробно-рациональная функция. Определив
-преобразования стоит дробно-рациональная функция. Определив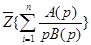 так, как излагалось выше (используя разложение выражения на простейшие дроби), можно легко найти Z -передаточную функцию разомкнутой системы.
так, как излагалось выше (используя разложение выражения на простейшие дроби), можно легко найти Z -передаточную функцию разомкнутой системы.
В общем случае для определения Z-передаточной функции W(z) можно использовать зависимость, полученную ранее в курсе «Математические основы ТАУ»:
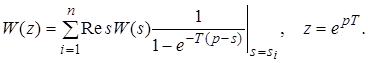 (20)
(20)
где si – полюсы передаточной функции W(s) ПНЧ ( 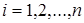 ).
).
Следует, однако, иметь в виду, что формула (20) справедлива, если выполняется условие
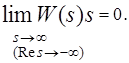 (21)
(21)
Например, если передаточная функция ПНЧ имеет вид 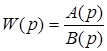 и степень многочлена
и степень многочлена 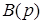 превосходит степень
превосходит степень 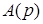 не менее чем на 2 порядка, то условие (21 выполняется, и тогда из зависимости (20) получим
не менее чем на 2 порядка, то условие (21 выполняется, и тогда из зависимости (20) получим
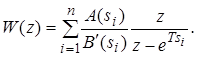 (22)
(22)
В случае, если передаточная функция ПНЧ содержит выражение 1-е-Tp, ее можно представить в виде
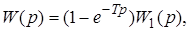
где 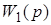 - дробно-рациональная функция.
- дробно-рациональная функция.
Тогда
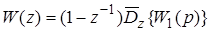
и
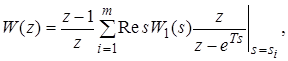 (23)
(23)
где 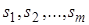 - полюсы функции
- полюсы функции 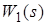 .
.
Дата добавления: 2016-07-05; просмотров: 2255;











