Передаточная функция разомкнутой импульсной системы.

3апишем теперь уравнения разомкнутой системы в изображени­ях. Применим к зависимости (10) Z-преобразование, С учетом свойств Z-преобразования найдем

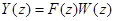, (11)

где Y(z)=Z{y[nT]}, F(z)=Z{f[nT]},W(z)=Z{w[nT]}.

Определим Z -передаточную функцию импульсной системы как отношение Z -преобразования выходной величины к Z -преоб­разованию входной величины при нулевых начальных условиях:

.

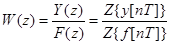Из уравнения (11) следует, что Z -передаточная функ­ция разомкнутой импульсной системы равна Z -преобразованию дискретной весовой функции w[nT] ПНЧ. т.е.

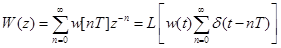. (12)

Формула (12) используется при вычислении Z -передаточных функ­ций разомкнутых импульсных систем.

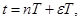
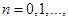
Иногда возникает необходимость определить реакцию системы в смещенные дискретные моменты времени 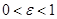. Подставив в зависимость (9) 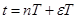, 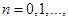получим

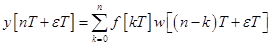(13)

Перейдя к уравнению в изображениях, найдем

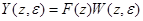(14)

Здесь изображения 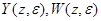соответствуют модифицированному Z-преобразованию решетчатых функций , 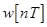. Уравнению (14) соответствует передаточная функция

,

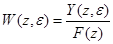cвязывающая модифицированное Z-преобразование выходного сигнала и обычное Z-преобразование входной переменной. При изменении параметра 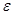от 0 до 1 зависимости (13), (14) позволяют определить значение выходной величины в любой промежуточный момент времени.