Уравнения разомкнутой импульсной системы.

В соответствии с определением ИИЭ имеем

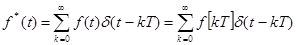. (6)

Выходной сигнал в силу свойства линейности можно рассматривать как сумму реакций приведенной непрерывной части на модулированную последовательность d–функций (6). В соответствии с известной формулой для непрерывных линейных систем при нулевых начальных условиях получим

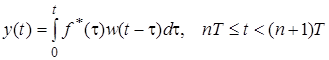
или с учетом формулы (6)

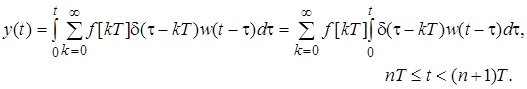(7)

Так как весовая функция 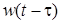, рассматриваемая по аргументу t, удовлетворяет условию

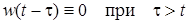
то

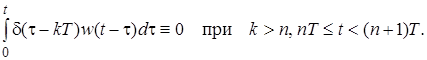
Таким образом, оба сомножителя под знаком интеграла отличны от нуля только при выполнении условия 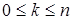. Для этих значений к в силу фильтрующего свойства d-функции найдем

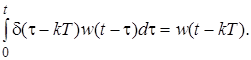(8)

Так как имеет смысл рассматривать только значения к, не превосходящие n, то в выражении (7) можно заменить верхний предел суммирования. Окончательно с учетом формулы (8) получим

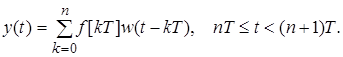(9)

При этом в дискретные моменты времени t=nT , n=0,1,… будем иметь

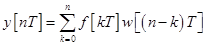. (10)

Уравнение (10) представляет собой уравнение импульсной системы во временной области, позво­ляющее определить выходной сигнал системы при известном вход­ном воздействии.